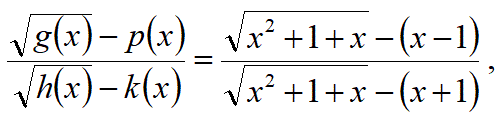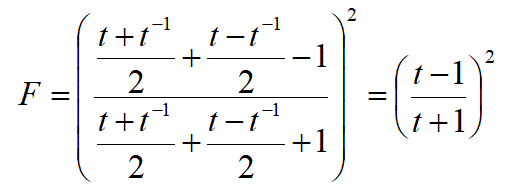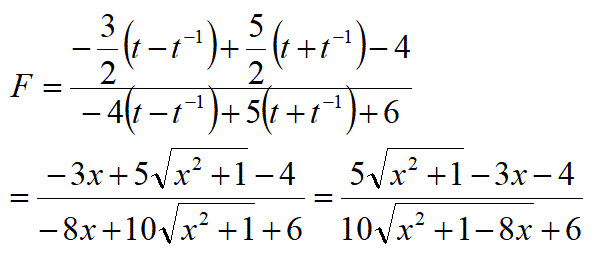無理関数の分数式の変換公式

以下は、ここをクリックした先の問題の解答です。

【問１】以下の、無理関数の分数式の変換公式を証明せよ。
ある定数Cで結ばれる、

という式の関係がある場合に、
その式に関係する以下の式（左辺の分数式）が、

右辺の分数式と等しい事を示せ。

【問２】以下の式が成り立つ事を示せ。

【問３】以下の式が成り立つ事を示せ。

【問４】以下の式が成り立つ事を示せ。

【問４ｂ】以下の式が成り立つ事を示せ。

【問４ｃ】以下の式が成り立つ事を示せ。


【問５】以下の式が成り立つ事を示せ。
ただし、ｘ≧１とする。

【問６】以下の式が成り立つ事を示せ。
ただし、ｘ≧１とする。

【問７】以下の式が成り立つ事を示せ。

【問１】以下の、無理関数の分数式の変換公式を証明せよ。
ある定数Cで結ばれる、

という式の関係がある場合に、
その式に関係する以下の式（左辺の分数式）が、

右辺の分数式と等しい事を示せ。

【問１の解答】

となる。
∴

が成り立つ。
（解答おわり）

【問２】以下の式が成り立つ事を示せ。

【問２の解答】

と置くと、
問１の関係で、C＝１の場合の関係が成り立っている。
よって、

が成り立つ。
（解答おわり） 

【問３】以下の式が成り立つ事を示せ。

【問３の解答】

と置くと、
問１の関係で、C＝－３の場合の関係が成り立っている。
よって、

が成り立つ。
（解答おわり）

問１の式は、公式として覚えてください。

　式の変形の過程で以上の形の式が出てきたら、すぐ、このように式を変形できるように式の変形のコツを覚えておいてください。

【問４】以下の式が成り立つ事を示せ。

【問４の解答（その１）】

と置く。
ただし、ｔ＞０とする。
すると：

が成り立つ。
これらの式を使って以下の様に計算する。

（解答（その１）おわり）

【問４の解答（その２）】


（解答（その２）おわり）

【問４ｂ】以下の式が成り立つ事を示せ。

【問４ｂの解答】

（解答おわり）

【問４ｃ】以下の式が成り立つ事を示せ。


【問４ｃの解答】

（解答おわり）

【問５】以下の式が成り立つ事を示せ。
ただし、ｘ≧１とする。

【問５の解答】

と置く。
ただし、ｔ≧１とする。
すると：

が成り立つ。
これらの式を使って以下の様に計算する。

（解答おわり）

【問６】以下の式が成り立つ事を示せ。
ただし、ｘ≧１とする。

【問６の解答】

と置く。
ただし、ｔ≧１とする。
すると：

が成り立つ。
これらの式を使って以下の様に計算する。

上式の形を成り立たせる係数Ａ，Ｂ，Ｃ，Ｄを求める。

 この係数を代入して計算を続ける。

（解答おわり）

【問７】以下の式が成り立つ事を示せ。

【問７の解答】

と置く。
ただし、ｔ＞０とする。
すると：

が成り立つ。
これらの式を使って以下の様に計算する。

上式の形を成り立たせる係数Ａ，Ｂ，Ｃ，Ｄを求める。

 この係数を代入して計算を続ける。

（解答おわり）

リンク：
高校数学の目次