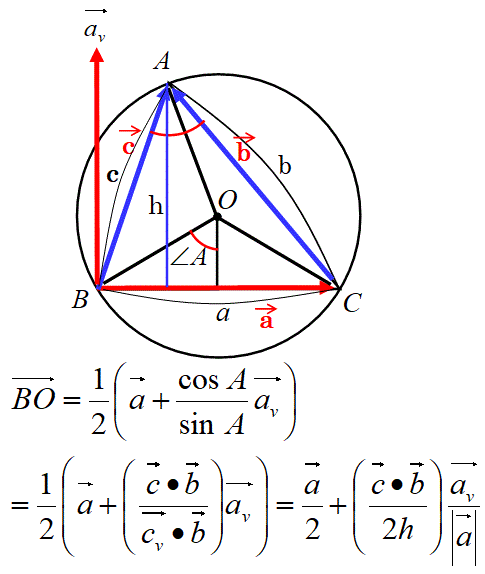これは、ここをクリックした先の問題の解答です。
【一番簡単な解き方の秘訣】
(あるベクトルmとcとが互いに垂直であるという条件のある図形の問題を解くときは、
(1)それらのベクトルmとcを、互いに垂直な単位ベクトルxとyの合成であらわして(ただし、ベクトルxは三角形の所定の辺の方向に平行。ベクトルyはその辺に垂直な方向を向く)、
(2)そして、ベクトルmとcが垂直である条件として内積が0であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。)
【解答1】
以下の図のような三角形ABCを考えて、ベクトル方程式を解いてベクトルMOの解の公式を計算する。

ここで、互いに直交するベクトルxとyと未知数mでベクトルMO等をあらわす。このときベクトルDOとベクトルcが直交するベクトル方程式を作って、それを解きます。
(解答1おわり)
【解答2】
互いに直交する基準ベクトルをベクトルaとベクトルav にして計算することができる。ベクトルcと同時にそれに垂直なベクトルcv が存在して同時に定義できると考える。そうすると、ベクトルBOが、以下の式であらわせる。
(解答2おわり)
(補足)
三角形ABCの面積をSとすると、以下の式で面積Sがあらわせるからです。

リンク:
高校数学の目次
【一番簡単な解き方の秘訣】
(あるベクトルmとcとが互いに垂直であるという条件のある図形の問題を解くときは、
(1)それらのベクトルmとcを、互いに垂直な単位ベクトルxとyの合成であらわして(ただし、ベクトルxは三角形の所定の辺の方向に平行。ベクトルyはその辺に垂直な方向を向く)、
(2)そして、ベクトルmとcが垂直である条件として内積が0であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。)
【解答1】
以下の図のような三角形ABCを考えて、ベクトル方程式を解いてベクトルMOの解の公式を計算する。

ここで、互いに直交するベクトルxとyと未知数mでベクトルMO等をあらわす。このときベクトルDOとベクトルcが直交するベクトル方程式を作って、それを解きます。
(解答1おわり)
【解答2】
互いに直交する基準ベクトルをベクトルaとベクトルav にして計算することができる。ベクトルcと同時にそれに垂直なベクトルcv が存在して同時に定義できると考える。そうすると、ベクトルBOが、以下の式であらわせる。
(解答2おわり)
(補足)
三角形ABCの面積をSとすると、以下の式で面積Sがあらわせるからです。

リンク:
高校数学の目次