これは、ここをクリックした先の問題の解答です。
【問1】
Aと書かれたカード、Bと書かれたカード、Cと書かれたカードがそれぞれ2枚の計6枚を円形に並べたとき、1部分でも、時計回りにABCと続いて並ぶ確率を求めよ。
【解答】
この種の問題は、以下の様に地道に場合分けして確率を求めることができます。
A1,A2,B1,B2,C1,C2の6枚のカードを円形にならべる。
(各カードの模様をA,B,C,Dとする。
模様Bの個々の2つのカードB1,B2 のどれか1つをBxと書き、残りの1つのカードをByであらわす。)
A1の位置を固定する。
時計回りに、A1に続いて並ぶうち、ABCと続いて並ぶ確率を、以下の樹形図を使って計算する。
《事象の連鎖の表現》
下図の樹形図では、A1と、それに続くカードの順列によって事象の連鎖をあらわす。
例えば、事象の連鎖をA1,A2,Bx,Cy,残5,残6とあらわす。その事象の連鎖の、カードが不定な部分の表現を省略してA1,A2,Bx,Cyであらわす。
また、事象の連鎖をA1,Bx,Cy,残4,残5,残6とあらわす。その事象の連鎖の、カードが不定な部分の表現を省略してA1,Bx,Cyであらわす。

(解答おわり)
リンク:
高校数学の目次
これは、ここをクリックした先の問題の解答です。
【問1】
A,B,C,D,a,bを円形に並べるとき
(1)4個の大文字のうち3個だけが隣り合う確率
(2)Aとa,およびBとbがそれぞれ向かい合う確率
を求めよ。
【解答1】
この問題は、回転させてみると形が6つに変わる問題なので、
回転させて形が重なる形6つを1つの形で代表させることで問題を簡単にします。
(1)の解答:
下図の①から③まで、図形をいろいろ書いて考える。
③では、文字を配置する席(位置)の形をみつける。
④で、その席の形も、回転させてみると形が6つに変わる事を確認する。
その席の形が6つに変わるので、その形が重なる6つの席の形を③でみつけた席の形で代表させる。
上図のように、③の形の席に文字を配置する場合の数を数える。
その場合の数を、回転させて重なる形の代表の総数で割り算して、求める確率を求める。
((1)の答え)確率=2/5
((1)の解答おわり)
(2)の解答:
下図の①から②まで、図形をいろいろ書いて考える。
②では、文字を配置する席(位置)の形をみつける。
③で、その席の形も、回転させてみると形が6つに変わる事を確認する。
その席の形が6つに変わるので、その形が重なる6つの席の形を②でみつけた席の形で代表させる。
上図のように、②の形の席に文字を配置する場合の数を数える。
その場合の数を、回転させて重なる形の代表の総数で割り算して、求める確率を求める。
((2)の答え)確率=1/15
((2)の解答おわり)
【解答1の2】
以下の様に、同様に計算して解答できます。
(問題を易しくする)
円上に文字を順に並べるパターンの発生確率を求める問題は、同じパターン(ただし、その位置が回転している)が重複して生じます。同じものが回転して形を変えて現れるなら、その全部を1つの物と把握して、問題を、より単純な問題に変換できないかと考えます。
(解決策)
この問題は、6文字全てが異なる文字なので、どれかの第1の文字(その文字を仮にXとする)の位置を固定した配列パターンを考えれば、そのパターンは、その配列全体を回転させた、文字Xが6か所にある6つのパターンを代表したパターンになります。それにより、考えなければいけない配列パターンの数を6分の1に単純化できます。
その配列パターンの数は、
固定した文字以外の5つの文字を文字Xから右回りに配置する組み合わせなので、
5!=5×4×3×2×1=120通り
(1)の解答
4個の大文字のうち他の大文字と隣り合わない1個の文字Xを決め、その位置を固定します。
・・・文字Xの選び方は4通り。
文字Xの両隣は小文字2つですから、
その小文字2つの並べ方は2通り。
最後に隣り合う大文字3個の組を置きますが、
大文字3個の並べ方は
3×2×1=6通りあります。
従って
4×2×6=48通り。
確率は、48/120=2/5
((1)の解答おわり)
(2)の解答
Aを決めます・・・1通り
aは自動的にきまります。
Bを決めますが、残りの場所は4つなので・・・4通り
bは自動的にきまります。
残り2つの場所にC,Dを並べます・・・2通り
従って、1×4×2=8通り
確率は、8/120=1/15
((2)の解答おわり)
「教科書より詳しい高校数学」
の「円形に並べる確率」の解説も参考になります。
「円順列の求め方は「固定させる!」でしたが条件が付くことによって解法が変わります。それぞれのパターンをしっかりと理解しておきましょう。」
【解答2】
確率という視点で考えると、以下の様な発想も可能になります。
この解き方は、以下の様に発案して解く事ができると思います。
(1)の問題は、文字の並び方が、「4個の大文字のうち3個だけが隣り合う確率」という表現で、大文字に注目させた問題です。しかし、そういう問題だからこそ、逆転の発想で、問題文では注目させられず陰に隠れている小文字に注目してみましょう。
(第1に)
小文字aの位置を固定します。
(第2に)
小文字aの位置を固定すれば、あと、残っている小文字はbのみです。その小文字bの位置によって、大文字の配列の形が決まってしまいます。
(考察)
大文字のうち3個だけが隣り合うパターンを決める小文字bの位置とはどこかと考えてみます。小文字bの配置できる位置は小文字aの位置以外の5か所のみです。
その5か所を全て考えると、2か所のみが、(1)の問題の条件を満足する事がわかります。
そのため、(1)の問題の解答は、小文字bが5か所のうち2か所に配列される確率だとわかりました。
((1)の解答)
小文字aの位置を固定点にして、回転して重なる文字配置の代表にする。
すると、小文字bの配置できる点は5つある。
その配置できる点のうち、小文字aから1文字おいた次の位置(それは2つある)に小文字bを置く場合のみに、3個の大文字だけが隣り合う配置になる。
その位置の小文字bを置く確率=2/5である。
((1)の解答おわり)
((2)の問題の解き方)
(2)の問題も、「Aとa,およびBとbがそれぞれ向かい合う確率を求めよ」と表現され、大文字に注目させた問題です。しかし、そういう問題だからこそ、逆転の発想で、問題文では注目させられず陰に隠れている小文字に注目してみましょう。「aとA、および、bとBがそれぞれ向かい合う確率を求めよ」という問題に変換して考えます。
小文字はaとbとの2つしかありませんので、その2つに係る事だけを考えれば良いので、問題が簡単になります。
(考察1)
小文字aの位置を固定します。すると、aの位置に対向する位置も固定されます。
その固定された位置に文字Aが来る確率とは何かを考えます。
文字Aの位置の自由度は、小文字aの位置以外の5か所のみです。そのうち、小文字aの位置に対向する位置は1か所しかありません。
そのため、
小文字aの位置に対向する位置に文字Aが来る確率は、
1/5
だとわかります。
(考察2)
小文字aと大文字Aを配置した後で、
小文字bの位置に対向する位置に文字Bを配置する確率を考えます。
小文字bの位置が決まらなければ、その位置に対向する位置も定まりませんが、
分かっている事は、小文字bの配置できる位置は、小文字aと大文字Aの位置以外の4か所の位置のどこかに配置される事です。
そして、小文字bを配置したら、大文字Bが配置できる位置は3か所しか無い事です。
小文字bの位置がどこであっても、その小文字bの位置に対向する位置は存在し、その位置は1か所のみです。
そのため、
小文字aと大文字Aを配置し、更に、小文字bを任意の可能な位置に配置した後に、
小文字bの位置に対向する位置に文字Bを配置する確率は、
1/3
です。
以上の考察により、(2)の問題は、以下の様に解く事ができることがわかりました。
((2)の解答)
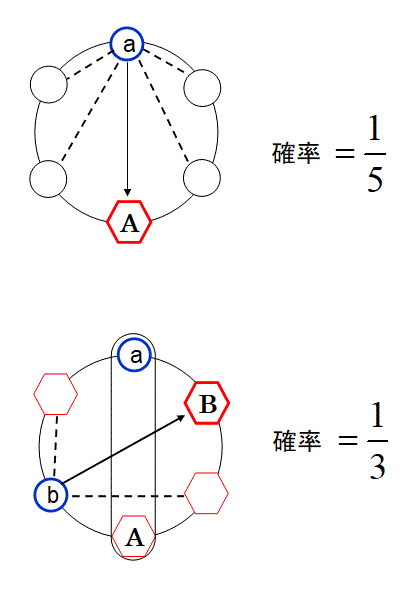
小文字aの位置を固定点にすると、
大文字Aが小文字aに対向する位置に来る確率=1/5である。
大文字Aが小文字aに対抗する位置にあって、残りの位置4つのどこかに小文字bがある場合に、大文字Bの配置できる点は3つある。
その配置できる点のうち、小文字bに対向する位置に来る確率=1/3である。
よって、
大文字Aが小文字aに対向する位置に来て、かつ、大文字Bが小文字bに対向する位置に来る確率
=(1/5)×(1/3)=1/15である。
((2)の解答おわり)
(補足1)
(2)の問題では、先ず文字aを配置し、次に文字Aを配置し、次に文字bを配置し、次に文字Bを配置する、という文字の配置の順番を自分で勝手に定めて、その順番で配置する場合に目的の配置パターンに近付いていく確率を求めました。
その様に、自分で勝手に定めた順に文字を配置して確率を求める方法でも正しい確率の答えが得られるという原理を使って問題を解きました。
この原理は、この様にして問題を解いても正しい答えが得られるという経験からつかみ取った原理です。
(補足2)
確率の問題は、パターンの要点のみに注目して確率を求める解答2の様な発想で問題を解く事ができます。
解答1のように全ての場合を数え上げないでも解ける道があるのが確率の問題の特徴です。
リンク:
高校数学の目次