【問1】(1)以下の関数の逆関数を求めよ。
(2)上の式の根号であらわした項をyで表せ。
【問2】以下の関数の逆関数を求めよ。
【問3】(1)以下の関数の逆関数を求めよ。
(2)上の式の根号であらわした項をyで表せ。
【問4】以下の関数の逆関数を求めよ。
【問5】以下の関数の逆関数を求めよ。

【問6】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【問7】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【問1】(1)以下の関数の逆関数を求めよ。
(2)上の式の根号であらわした項をyで表せ。
【問1の解答(その1)】
(1)
ただし、y>0
(解答(その1(1))おわり)
(2)
(解答(その1(2))おわり)
【問1の解答(その2)】


(解答(その2)おわり)
【問2】以下の関数の逆関数を求めよ。
【問2の解答(その1)】
【問2の解答(その2)】


(解答(その2)おわり)
【問3】(1)以下の関数の逆関数を求めよ。
ただし、x≧1とする。
(2)上の式の根号であらわした項をyで表せ。
【問3の解答】
(1)
この解のxは、 上図のグラフの赤線で囲った部分のyで表される。
(解答おわり)
(2)
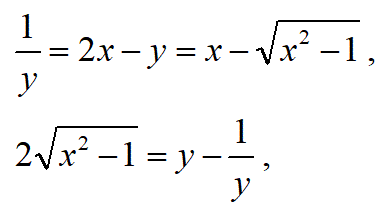
(解答おわり)
(補足)この問3で、
x<0の場合の逆関数は、以下のように解ける。
【解答】
この解のxは、上図のグラフの赤線で囲った部分のyで表される。
(解答おわり)
-1≦y<0,と1≦yの範囲を使うことで、
x≧1の場合とx≦-1の場合に共通に:
x=(1/2)(y+(1/y))
の式で逆関数があらわされる。
また、
y(-x)=-1/y(x),
の関係がある。
【問4】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【問4の解答】
グラフから、y≦1が分かる。
(解答おわり)
(補足)この問4で、
x<0の場合の逆関数は、以下のように解ける。
0<y≦1,とy≦-1の範囲を使うことで、
x≧1の場合とx≦-1の場合に共通に:
x=(1/2)(y+(1/y))
の式で逆関数があらわされる。
【問5】以下の関数の逆関数を求めよ。

【解答】
x≧0のときy≧0,
x≦0のときy≦0,
この関数のグラフを描くと以下の図になります。
(図の変数は、上式の変数x,yと異なるので注意)
【問6】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【解答】
(ただし、y≧0)
(解答おわり)
【問7】以下の関数の逆関数を求めよ。
ただし、x≧1とする。
【解答】
よって、y≦0
(解答おわり)
リンク:
高校数学の目次



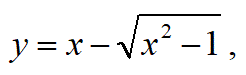




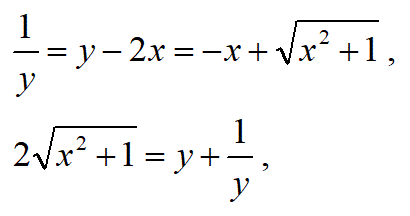



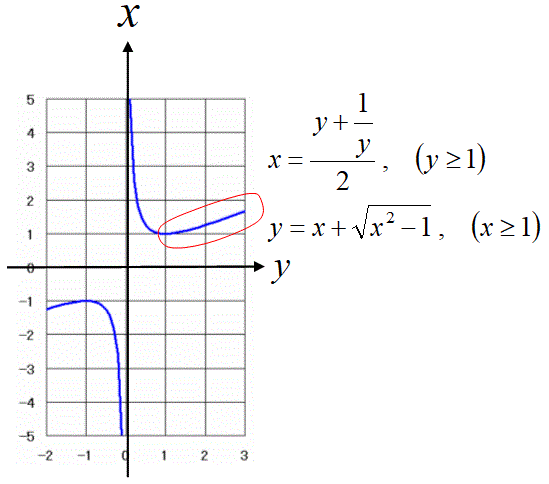


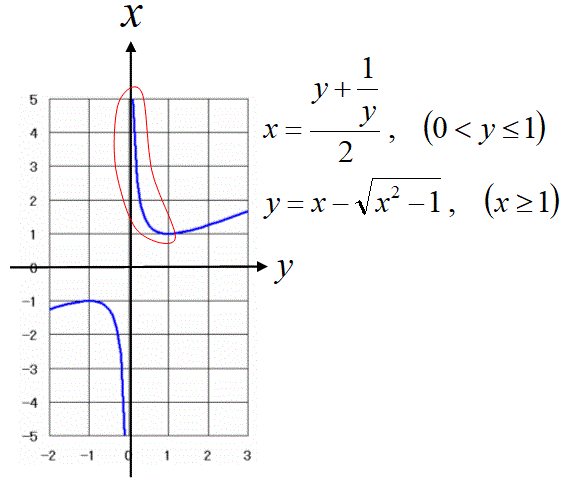






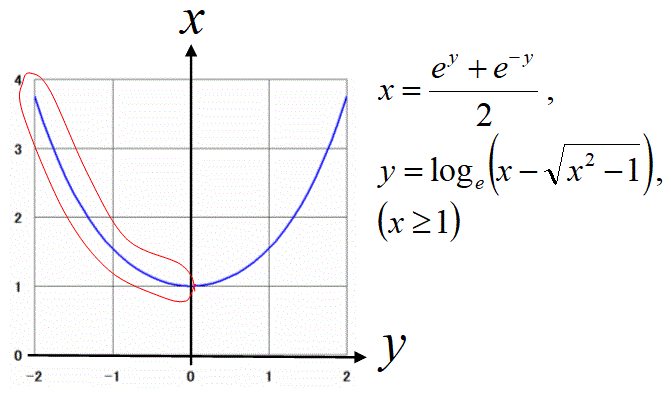
0 件のコメント:
コメントを投稿