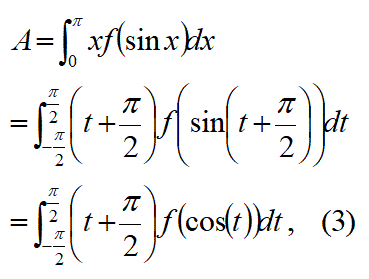以下は、ここをクリックした先の問題の解答です。
【問1】
f(x)を連続関数とすると、
が成り立つことを示せ。
【解答1】
関数の対称性を利用するため、変数xを以下の式2で定義する変数tに変換して、tの対称な積分範囲で積分する。
式1の左辺は以下の式に変換できる。
ここで、関数の対称性を利用する。
式3の第1項(式4の左辺)は、t・f(cos(t))の積分である。
cos(t)はtに関して、cos(-t)=cos(t)となる対称関数(偶関数)である。
そのため、f(cos(t))も、tに関して対称な関数(偶関数)になる。
一方、関数 t は、tに関して反対称な(tの符号が正負逆になれば、値も正負逆になる)関数(奇関数)である。
tに関して対称な関数と、tに関して反対称な関数の積は、tに関して反対称な関数(奇関数)になる。
そのため、t・f(cos(t))は、tに関して反対称な関数(奇関数)である。
tに関して反対称な関数(奇関数)を、対称な範囲[-a,a]で積分すれば、積分結果は0になる。
式3の第1項は、反対称な関数(奇関数) t・f(cos(t))を対称な範囲で積分しているので、式4のように、その積分結果は0になる。
そのため、積分Aは以下の式で計算できる。
(解答1おわり)
【解答2】
関数の対称性を利用するため、変数xを以下の式2で定義する変数tに変換して、tの対称な積分範囲で積分する。
式1の左辺は以下の式3に変換できる。
ここで、この被積分関数のtを-tに置き換えた関数は、t=0となるy軸を鏡にした左右逆の関数になり、左右が入れ替わった関数になるが、
左右が逆という事以外は同じ形の関数になるので、
それをtの対称な積分範囲で積分した値も同じ値Aになる。
よって、積分Aは、式3の関数の積分Aと、tを-tに置き換えた関数の積分Aを加えて2で割り算した値になる。
(解答2おわり)
【解答2の2】
解答2の式3の後の計算は、以下の様に計算することもできる。
(解答2の2おわり)
【解答3】
解答2の様に、「関数の積分は、その関数を左右を逆にした関数の積分と等しい」という事を使って、その2つの関数の和の平均値で積分を求める。
そのため、先ず、「関数の積分は、その関数を左右を逆にした関数の積分と等しい」という事(当たり前だとは思うが)を以下の様に証明して用いる。
この式5によって、「関数の積分は、その関数を左右を逆にした関数の積分と等しい」事が証明できた。
そのため、以下の式で積分Aを求める。
(解答3おわり)
【解答4】
解答1で変数xを変数tに変換して計算する計算を、下図のように、関数の対称軸をY軸から、x=π/2 の軸に移動させて、その対称軸を基準にして関数を考える。
被積分関数を、この対称軸に関して対称な関数成分と反対称な関数成分に分けて考える。
それは、y=xという関数を、
y=π/2という関数と、
y=x-π/2という関数
に分割する事で行なえる。
対称な関数の成分についてのみ積分すれば、式1の左辺の積分が、
式1の右辺の積分になる。
(解答4おわり)
リンク:
高校数学の目次
【問1】
f(x)を連続関数とすると、
が成り立つことを示せ。
【解答1】
関数の対称性を利用するため、変数xを以下の式2で定義する変数tに変換して、tの対称な積分範囲で積分する。
式1の左辺は以下の式に変換できる。
ここで、関数の対称性を利用する。
式3の第1項(式4の左辺)は、t・f(cos(t))の積分である。
cos(t)はtに関して、cos(-t)=cos(t)となる対称関数(偶関数)である。
そのため、f(cos(t))も、tに関して対称な関数(偶関数)になる。
一方、関数 t は、tに関して反対称な(tの符号が正負逆になれば、値も正負逆になる)関数(奇関数)である。
tに関して対称な関数と、tに関して反対称な関数の積は、tに関して反対称な関数(奇関数)になる。
そのため、t・f(cos(t))は、tに関して反対称な関数(奇関数)である。
tに関して反対称な関数(奇関数)を、対称な範囲[-a,a]で積分すれば、積分結果は0になる。
式3の第1項は、反対称な関数(奇関数) t・f(cos(t))を対称な範囲で積分しているので、式4のように、その積分結果は0になる。
そのため、積分Aは以下の式で計算できる。
(解答1おわり)
【解答2】
関数の対称性を利用するため、変数xを以下の式2で定義する変数tに変換して、tの対称な積分範囲で積分する。
式1の左辺は以下の式3に変換できる。
ここで、この被積分関数のtを-tに置き換えた関数は、t=0となるy軸を鏡にした左右逆の関数になり、左右が入れ替わった関数になるが、
左右が逆という事以外は同じ形の関数になるので、
それをtの対称な積分範囲で積分した値も同じ値Aになる。
よって、積分Aは、式3の関数の積分Aと、tを-tに置き換えた関数の積分Aを加えて2で割り算した値になる。
(解答2おわり)
【解答2の2】
解答2の式3の後の計算は、以下の様に計算することもできる。
(解答2の2おわり)
【解答3】
解答2の様に、「関数の積分は、その関数を左右を逆にした関数の積分と等しい」という事を使って、その2つの関数の和の平均値で積分を求める。
そのため、先ず、「関数の積分は、その関数を左右を逆にした関数の積分と等しい」という事(当たり前だとは思うが)を以下の様に証明して用いる。
この式5によって、「関数の積分は、その関数を左右を逆にした関数の積分と等しい」事が証明できた。
そのため、以下の式で積分Aを求める。
(解答3おわり)
【解答4】
解答1で変数xを変数tに変換して計算する計算を、下図のように、関数の対称軸をY軸から、x=π/2 の軸に移動させて、その対称軸を基準にして関数を考える。
被積分関数を、この対称軸に関して対称な関数成分と反対称な関数成分に分けて考える。
それは、y=xという関数を、
y=π/2という関数と、
y=x-π/2という関数
に分割する事で行なえる。
対称な関数の成分についてのみ積分すれば、式1の左辺の積分が、
式1の右辺の積分になる。
(解答4おわり)
リンク:
高校数学の目次