以下は、ここをクリックした先の問題の解答です。
【問題2】
以下の関数 h(x)を微分せよ。
ただし、x>0とする。
【解1】
両辺の対数をとり、微分する。
(解1おわり)
【解2】
解1の式2から、h(x)を、変数xを完全に媒介変数sに置き換えて、sだけで表した関数m(s)が得られる。
そのため、この関数m(s)を使った合成関数の微分の公式が使える。
更に、この関数m(s)を、変数sを完全に媒介変数uに
置き換えて、uだけで表した関数 g(u)が得られる。
そのため、この関数 g(u) を使った合成関数の微分の公式が使える。
よって、以下の合成関数の微分の公式の連鎖の計算ができる。
(解2おわり)
リンク:
高校数学の目次
以下の関数 h(x)を微分せよ。
ただし、x>0とする。
【解1】
両辺の対数をとり、微分する。
(解1おわり)
【解2】
解1の式2から、h(x)を、変数xを完全に媒介変数sに置き換えて、sだけで表した関数m(s)が得られる。
そのため、この関数m(s)を使った合成関数の微分の公式が使える。
更に、この関数m(s)を、変数sを完全に媒介変数uに
置き換えて、uだけで表した関数 g(u)が得られる。
そのため、この関数 g(u) を使った合成関数の微分の公式が使える。
よって、以下の合成関数の微分の公式の連鎖の計算ができる。
(解2おわり)
リンク:
高校数学の目次




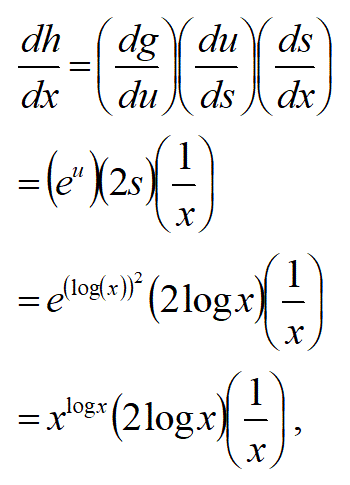
0 件のコメント:
コメントを投稿