単位ベクトルの要素の２乗の差の公式

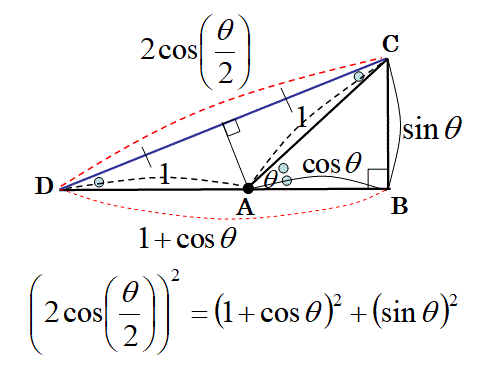
以下は、ここをクリックした先の問題の解答です。

単位ベクトルＡ（ａ_１，ａ_２）と単位ベクトルＢ（ｂ_１，ｂ_２）について、 以下の公式を証明せよ。


【問１】以下の公式を証明せよ。

（証明開始）

（証明おわり）

【問２】以下の公式を証明せよ
ａ_１^２ｂ_２^２－ ａ_２^２ｂ_１^２ ＝ａ_１^２－ｂ_１^２

（証明開始）
ａ_１^２ｂ_２^２－ ａ_２^２ｂ_１^２
＝ ａ_１^２ｂ_２^２ ＋（ａ_１^２ｂ_１^２－ａ_１^２ｂ_１^２） －ａ_２^２ｂ_１^２
＝ａ_１^２（ｂ_２^２＋ｂ_１^２） －（ａ_１^２＋ａ_２^２）ｂ_１^２
＝ａ_１^２－ｂ_１^２
＝－ａ_２^２＋ｂ_２^２ 
（証明おわり） 

これらは、公式として覚えてください。
（これらの単位ベクトルの要素をｓｉｎとｃｏｓであらわして公式をあらわすこともできます。） 

　式の変形の過程で以上の形の式が出てきたら、すぐ、このように式を変形できるように式の変形のコツを覚えておいてください。

リンク：
高校数学の目次

二等辺三角形の底辺の長さ

これは、ここをクリックした先のページの問題の解答です。

【問題】 
以下の二等辺三角形ACDの底辺CDの長さXを頂角Aのsinθとcosθを使ってあらわせ。

【解答】
以下の様に図のBDの長さを書いて、三平方の定理を使ってXの２乗を計算する。

よって、

である。

（解答おわり）
リンク：
高校数学の目次

頂角が半分の三角形の三平方の定理の変換

これは、ここをクリックした先のページの問題の解答です。

【問題】 
三角形の頂角を半分にした三角形に関して、
以下の式１及び２が成り立つことを証明せよ：

【式１の証明開始】
以下の三角形DBCを書く。

 三角形DBCの三平方の定理の式を以下の様に変形する。

（証明おわり）

【式２の証明開始】
以下の三角形CBDを書く。

 三角形CBDの三平方の定理の式を以下の様に変形する。

（証明おわり）

リンク：
高校数学の目次