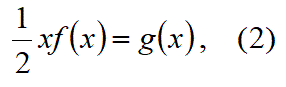積分方程式の問題

以下は、ここをクリックした先の問題の解答です。

以下の問題で言う連続関数とは、１つながりに連続な関数の事を意味するものとする。

【問１】
x≠0のときF(x)が微分可能であって、
F '(x)=0, (1)
が成り立つものとする。
x=0の点でF(x)が連続とは限らないとき、
F(x)を求めよ。

【解答】
ｘ＝０では関数F(x)の値が連続とは限らないので、F '(x)の値が存在しない。
そのためｘ＝０をまたいで関数F '(x)を積分することができない。
しかし、
ｘ＞０の範囲内のみならば積分が可能であり、
ｘ＜０の範囲内のみならば積分が可能である。
そのためそれらの区間毎に場合分けして、関数F '(x)を積分する。

(A) ｘ＞０ の区間で、
F(x)=∫0dx=Ｃ,

(B) ｘ＜０　の区間で、
F(x)=∫0dx=Ｅ,

(C) ｘ＝０　で、
F(x)=Ｈ,
Ｃ，Ｄ，Ｈは任意の定数。
（解答おわり）

【問２】
f(x)が連続関数である場合で、
f(x)は微分可能であるとは限らないとき、

を満足するf(x)を求めよ。

【解答】

とする。
式１の左辺は連続関数の積分であるので、微分積分学の基本定理に従って微分可能である。
よって右辺のxf(x)=g(x)全体も微分可能である。
式１の左右の辺を微分する。


（A)場合分け　ｘ≠０　の場合：
(3)から、

現時点では、ｘ＝０では関数を考えない（定義しない）ので、
ｘ＝０をまたいだ関数の積分はできない。
しかし、
ｘ＞０の範囲内のみならば積分が可能であり、
ｘ＜０の範囲内のみならば積分が可能である。
そのためそれらの区間毎に場合分けして、式４の左右を積分して関数を調べる。

(A-1)　ｘ＞０　の場合：

Ｃは積分定数。

(A-2)　ｘ＜０　の場合：

Ｅは積分定数。

(B) ｘ＝０ の場合：
f(x)がｘ＝０でも連続な連続関数なので、

よって、
C=E=f(0),

(C)
x=0の場合も含め、
f(x)=C，
（解答おわり）

【問３】
関数f(x)が、関数値が無限大には発散しない関数である場合で、
f(x)は連続関数とは限らないとき、

を満足するf(x)を求めよ。

【解答】

とする。
式１の左辺は無限大には発散しない関数f(x)の積分であるので、リーマン積分が可能である。
その積分結果は連続関数になる。
よって右辺のxf(x)=g(x)全体も連続関数である。
ｘ≠０
で、f(x)も連続である。

（A)場合分け　ｘ≠０　の場合：
f(x)が連続である。

現時点では、ｘ＝０ではｆ(x)が連続とは限らないので、
式１の左辺で表されるf(x)の積分結果をｘ＝０では微分できない。
しかし、ｘ≠０の点では式１の左辺が微分できる。
そのため、ｘ≠０の点では式１の右辺も微分できる。

式１の左右の辺を微分する。

 
現時点では、ｘ＝０では関数を考えない（定義しない）ので、
ｘ＝０をまたいだ関数の積分はできない。
しかし、
ｘ＞０の範囲内のみならば積分が可能であり、
ｘ＜０の範囲内のみならば積分が可能である。
そのためそれらの区間毎に場合分けして、式４の左右の辺を積分して関数を調べる。

(A-1)　ｘ＞０　の場合：

Ｃは積分定数。

(A-2)　ｘ＜０　の場合：

Ｅは積分定数。

(B) ｘ＝０ の場合、
 
Ｈは積分定数。

各区間で、式５と６と７で定義された関数f(x)が式１を満足する
（解答おわり）

（補足）
この問３の解の関数 f(x) から、ｘ＝０における関数値を除去して、定義域をx≠０とした関数は、
定義域の全ての点で連続であるので、高校数学で教えられている連続関数になります。
しかし、
その関数は、正しい定義の連続関数では無い事に注意してください。

【問４】
f(x)が連続関数である場合で、
f(x)は微分可能であるとは限らないとき、

を満足する関数f(x)を求めよ。

【解答】

とする。
式１の左辺は連続関数の積分であるので、微分積分学の基本定理に従って微分可能である。
よって右辺が微分可能であり、関数g(x)=xf(x)の全体も微分可能である。
（f(x)は微分可能とは限らない）

式１の左右の辺を微分する。

（A)場合分け　ｘ≠０　の場合：
(3)から、

現時点では、ｘ＝０では関数を考えない（定義しない）ので、
ｘ＝０をまたいだ関数の積分はできない。
しかし、
ｘ＞０の範囲内のみならば積分が可能であり、
ｘ＜０の範囲内のみならば積分が可能である。
そのためそれらの区間毎に場合分けして、式４の左右の辺を積分して関数を調べる。

(A-1)　ｘ＞０　の場合：

Ｃは積分定数。
ここで、式５を式１に代入する。

(A-2)　ｘ＜０　の場合：

Ｅは積分定数。
ここで式８を式１に代入して、場合（Ａ-1）と同様に計算すると、
場合（Ａ-1）と同じ式７（ただし、ｘ＜０の場合）が得られる

(B) ｘ＝０ の場合：
f(x)が連続関数なので、場合（Ａ-1）と場合（Ａ-2)との極限値と関数値が一致し、

となり、
ｘ＝０の場合も、場合（Ａ-1）と同じ式７（ただし、ｘ＝０の場合）で関数値が表される。

(C)
x=0の場合も含めた全ての実数ｘで：

（解答おわり）

【問５】
関数f(x)が連続関数である場合で、
f(x)は微分可能とは限らないとき、

を満足するf(x)を求めよ。

【解答】

とする。
式１の左辺は連続関数の積分であるので、微分積分学の基本定理に従って微分可能である。
よって右辺のxf(x)=g(x)全体も微分可能である。
式１の左右の辺を微分する。

（A)場合分け　ｘ≠０　の場合：
(3)から、

現時点では、ｘ＝０では関数を考えない（定義しない）ので、
ｘ＝０をまたいだ関数の積分はできない。
しかし、
ｘ＞０の範囲内のみならば積分が可能であり、
ｘ＜０の範囲内のみならば積分が可能である。
そのためそれらの区間毎に場合分けして、式４の左右の辺を積分して関数を調べる。

(A-1)　ｘ＞０　の場合：

Ｃは積分定数。
ここで、式５を式１に代入する。

式５は（ｘ＞０で）式１を満足する。

(A-2)　ｘ＜０　の場合：

Ｅは積分定数。
ここで式６を式１の代入して場合(A-1)と同様に計算すると、場合(A-1)と同様に、式６が式１を満足することがわかる。

(B) ｘ＝０ の場合、
f(x)が連続関数なので、場合（Ａ-1）と場合（Ａ-2)との極限値と関数値が一致し、

となり、
f(0)=0
になる。
この関係は、 式５でも式６でも表せる。

各区間で、式５と６で定義され、ｘ＝０ではf(x)=0となる連続関数f(x)が式１を満足する
（解答おわり）

【問６】
関数f(x)が連続関数であり、かつ、微分可能なとき、

を満足するf(x)を求めよ。

【解答】

とする。
式１の左辺は連続関数の積分であるので、微分積分学の基本定理に従って微分可能である。
よって右辺のxf(x)=g(x)全体も微分可能である。
式１の左右の辺を微分する。

（A)場合分け　ｘ≠０　の場合：
(3)から、

現時点では、ｘ＝０では関数を考えない（定義しない）ので、
ｘ＝０をまたいだ関数の積分はできない。
しかし、
ｘ＞０の範囲内のみならば積分が可能であり、
ｘ＜０の範囲内のみならば積分が可能である。
そのためそれらの区間毎に場合分けして、式４の左右の辺を積分して関数を調べる。

(A-1)　ｘ＞０　の場合：

Ｃは積分定数。
ここで、式５を式１に代入する。

式５は（ｘ＞０で）式１を満足する。

(A-2)　ｘ＜０　の場合：

Ｅは積分定数。
ここで式６を式１の代入して場合(A-1)と同様に計算すると、場合(A-1)と同様に、式６が式１を満足することがわかる。

(B) ｘ＝０ の場合、
f(x)が連続関数なので、場合（Ａ-1）と場合（Ａ-2)との極限値と関数値が一致し、

となり、
f(0)=0
になる。
この関係は、 式５でも式６でも表せる。

各区間で、式５と６で定義され、ｘ＝０ではf(x)=0となる連続関数f(x)が式１を満足する
（解答おわり）

リンク：
高校数学の目次

tan(x/2)を変数tに置換する積分

以下は、ここをクリックした先の問題の解答です。

【問１】
以下の不定積分を求めよ。

【解１】
この問題を、
tan(x/2)=ｔとする変数ｔを正しく導入して以下の様に解きます。
（変数ｔを導入する考え方）
tan(x/2)=ｔ
とする変数ｔを導入する場合は、
「ここをクリックした参考サイトの様な解き方」
をすると、
x/2=π/2の点で、
tan(x/2)の値が無限大になってしまうので、
その点を含む x の区間では積分できない
という問題があります。
（ここをクリックした先の「広義積分を必要とする積分の例」を参照）
　この問題が積分の計算に障害を生じ無いようにするには、
被積分関数の

の分母が０になって、この被積分関数が積分できない場合に合わせて、
その場合が、tan(t/2)の値が無限大になる場合でもあるようにすると良いのです。
すなわち、
以下の様に計算します。

この変数ｔがπになる点で式５の積分ができない。
そのｔの値のときが、
u=tan(t/2)の値が無限大になる場合でもあるように、置換積分するための変数 u を整合すると良いのです。
すなわち、以下の様に計算します。

このように、
変数ｕによる変数ｔの制限条件の式８を、被積分関数の積分の制限条件の式６に整合させます。
こうしておいて、以下のように、計算の準備をします。

こうして準備した上で、
以下の積分の計算をします。

（解１おわり）

（補足１）
　なお、この積分では、変数変換をして、
被積分関数を、
１／sin(t)の t による積分に変換した上で、
tan(t/2)=u
とする変数 u を導入した計算をしました。
このような形に被積分関数を変換することが、この置換積分のコツです。

　なお、式１３の形の式は、「三角関数の分数式の変換公式」の公式４の式７や式６の様に、異なる三角関数の式に書き換える事もできます。
（補足１おわり） 

（補足２）
この計算で求めた以下の式は公式として覚えておくと便利だと思います。

この形の式は公式として覚えやすいと思います。
なお、この積分は、以下の式で表すこともできます。

この式は公式としては覚えにくいので覚える必要は無いと思います。
また、解がこの式で得られた場合に、その解を上の式のtan()の対数関数に変換して表す必要もないと考えます。
上の２つの式は互いに対等な解であると考えます。
（補足２おわり）

（補足３）
この問題の解の式１３で、
正確に不定積分を記述すると：
（１）0＜(x/2)+(π/6) ＜(π/2)　での式１３
（２）(π/2)＜(x/2)+(π/6) ＜(π)　での式１３
（３）(π)＜(x/2)+(π/6) ＜(3π/2)　での式１３
（４）(3π/2)＜(x/2)+(π/6) ＜(2π)　での式１３
・・・
という、異なる開区間の定義域で定義された無限個の不定積分の集まりの解であると書くのが正確な解の記述です。
（各不定積分の積分定数Cは、不定積分毎に異なります。）

この不定積分を使って
定積分
F(b)-F(a)
を計算する場合は、
各々の不定積分が定義されている開区間をはみだして定積分してはいけません。
異なる不定積分の定義域にまたがって
F(b)-F(a)
を計算してはいけないのです。
　積分が無限大まで進んで次に無限大を引き算して再び有限に戻って辻褄があうようにも見えますが、それは見せかけです。無限大から無限大を引き算して０になるという計算をしてはいけないのです。
（なお、不定積分は必ず１つながりに連続な関数になります。不定積分が１つながりに連続で無い点をまたがって関数を定積分しないようにしましょう。）
（補足３おわり）

【重要な注意】
　ここで、tan(x/2)=ｔとする変数ｔを導入する場合には、tan(x/2)が定義されていない（微分できない）x（例えばx＝π,3πなど）を積分の定義域から省く必要があります。
そのために、上の解き方のような技巧的な解き方をしました。
いつもそうしなければいけないとなると、tan(x/2)=ｔとする変数ｔを自由に導入して置換積分ができなくなります。

　しかし、それを改善する手段があります。
（１）　tan(x/2)が無限大になってその点のｘで積分できないので、その点以外で積分した結果を、バラバラな異なる積分の解とする。
（２）　そのバラバラな解同士が、その除外した点以外の積分の値の極限が、そのｘの点で接続できる場合は、関数の変数ｘの定義域を極限値を使って拡張します。それは広義積分と呼ばれています。それをするために、以下の説明文を解答に加えます。
「この関数F(x)のcos(x/2)→0とする極限のｘの値でのF(x)の極限値を、そのｘの値でのF(x)の値とする」
　この説明文を加えることにより、元の関数ではxの値が定義されていたが、tan(x/2)=ｔとする変数ｔを導入することで潰されたxの値を、広義積分によって定義域に復活させ、そのｘの値での関数F(x)の値を定義します。

　以下で、その方法による解を書きます。

【解２】
この問題を、
tan(x/2)=uとする変数uを直接的に導入して以下の様に解きます。

以下のように、変数uを定義し計算の準備をします。


次に、以下の置換積分の計算をします。




この関数F(x)のcos(x/2)→0となる極限のｘの値でのF(x)の極限値をそのxの値でのF(x)の値とする：


（解２おわり）

（補足）広義積分の適用について：
　上の式の計算は、式を同値変形するためには、式22のcos(x/2)≠0の制限条件を残して計算を続けるべきです。しかし、上の計算では、関数の極限値によって関数の値を定義する広義積分を使って、分母と分子にcos(x/2)を掛け算しました。このように、同値変形では無い式の変形を行なって、式22のx≠πの制限条件を解消しています。この計算は、積分とは無関係な式の計算では通用しないものです。そのため、上の式の積分結果を変形する式において、
「この関数F(x)のcos(x/2)→0となる極限のｘの値でのF(x)の極限値をそのxの値でのF(x)の値とする」
と一言書いてから式を変形すれば、このように同値変形では無い計算をしていることが減点されないと思います。

【解３】
「積分計算と相性が良い三角関数の積の分数の分解の公式」を用いて、以下のように計算することもできます。

ここで、「積分計算と相性が良い三角関数の積の分数の分解の公式」を適用する。

（解３おわり）

リンク：
高校数学の目次