以下は、ここをクリックした先の問題の解答です。
【問1】
以下の不定積分を求めよ。
【解1】
この問題を、
tan(x/2)=tとする変数tを正しく導入して以下の様に解きます。
(変数tを導入する考え方)
tan(x/2)=t
とする変数tを導入する場合は、
「ここをクリックした参考サイトの様な解き方」
をすると、
x/2=π/2の点で、
tan(x/2)の値が無限大になってしまうので、
その点を含む x の区間では積分できない
という問題があります。
(ここをクリックした先の「広義積分を必要とする積分の例」を参照)
この問題が積分の計算に障害を生じ無いようにするには、
被積分関数の
の分母が0になって、この被積分関数が積分できない場合に合わせて、
その場合が、tan(t/2)の値が無限大になる場合でもあるようにすると良いのです。
すなわち、
以下の様に計算します。

この変数tがπになる点で式5の積分ができない。
そのtの値のときが、
u=tan(t/2)の値が無限大になる場合でもあるように、置換積分するための変数 u を整合すると良いのです。
すなわち、以下の様に計算します。
このように、
変数uによる変数tの制限条件の式8を、被積分関数の積分の制限条件の式6に整合させます。
こうしておいて、以下のように、計算の準備をします。
こうして準備した上で、
以下の積分の計算をします。
(解1おわり)
(補足1)
なお、この積分では、変数変換をして、
被積分関数を、
1/sin(t)の t による積分に変換した上で、
tan(t/2)=u
とする変数 u を導入した計算をしました。
このような形に被積分関数を変換することが、この置換積分のコツです。
なお、式13の形の式は、「三角関数の分数式の変換公式」の公式4の式7や式6の様に、異なる三角関数の式に書き換える事もできます。
(補足1おわり)
(補足2)
この計算で求めた以下の式は公式として覚えておくと便利だと思います。
この形の式は公式として覚えやすいと思います。
なお、この積分は、以下の式で表すこともできます。
この式は公式としては覚えにくいので覚える必要は無いと思います。
また、解がこの式で得られた場合に、その解を上の式のtan()の対数関数に変換して表す必要もないと考えます。
上の2つの式は互いに対等な解であると考えます。
(補足2おわり)
(補足3)
この問題の解の式13で、
正確に不定積分を記述すると:
(1)0<(x/2)+(π/6) <(π/2) での式13
(2)(π/2)<(x/2)+(π/6) <(π) での式13
(3)(π)<(x/2)+(π/6) <(3π/2) での式13
(4)(3π/2)<(x/2)+(π/6) <(2π) での式13
・・・
という、異なる開区間の定義域で定義された無限個の不定積分の集まりの解であると書くのが正確な解の記述です。
(各不定積分の積分定数Cは、不定積分毎に異なります。)
この不定積分を使って
定積分
F(b)-F(a)
を計算する場合は、
各々の不定積分が定義されている開区間をはみだして定積分してはいけません。
異なる不定積分の定義域にまたがって
F(b)-F(a)
を計算してはいけないのです。
積分が無限大まで進んで次に無限大を引き算して再び有限に戻って辻褄があうようにも見えますが、それは見せかけです。無限大から無限大を引き算して0になるという計算をしてはいけないのです。
(なお、不定積分は必ず1つながりに連続な関数になります。不定積分が1つながりに連続で無い点をまたがって関数を定積分しないようにしましょう。)
(補足3おわり)
【重要な注意】
ここで、tan(x/2)=tとする変数tを導入する場合には、tan(x/2)が定義されていない(微分できない)x(例えばx=π,3πなど)を不定積分の定義域から省く必要があります。
そのために、上の解き方のような技巧的な解き方をしました。
いつもそうしなければいけないとなると、tan(x/2)=tとする変数tを自由に導入して置換積分ができなくなります。
しかし、それを改善する手段があります。
(1) tan(x/2)が無限大になってその点のxで積分できないので、不定積分の変数xの定義域を、そのxの点を境界点にしたその境界点以外の左側の区間を第1の不定積分の変数xの定義域にする。また、その境界点以外の右側の区間を第2の不定積分の変数xの定義域にする。そのように、定義域が異なる2つの不定積分の解を求める。
(2) そのように定義域がバラバラな不定積分の解同士が、そのxの境界点で、不定積分の有限な値の極限値があり、そのxの境界点で、第1と第2の不定積分の解が接続できる場合は、そのxの境界点での極限値をその不定積分の関数の値として定義する。それは広義積分と呼ばれている。広義積分をすることを明確にするために、以下の説明文を解答に加える。
「この不定積分の関数F(x)でのcos(x/2)→0となる変数xの極限でのF(x)の極限値を、そのxの値でのF(x)の値と定義する」
そして、xの境界点の左右の区間をつないで一体化して1つの区間にし、その区間を第1と第2の不定積分を合体させた関数F(x) の定義域にする。こうして、元の関数ではxの値が定義されていたが、tan(x/2)=tとする変数tを導入することで潰された変数xの値を、広義積分によってそのxの点での関数F(x)の値を定義することでそのxの点を定義域に復活させる。また、関数F(x) の定義域の区間を拡大する。
【解2】
この関数の積分を、
tan(x/2)=uとする変数uを直接的に導入して以下の様に置換積分して解きます。

先ず、被積分関数の分母が0になる、積分できないxの点を求める。

この値のxの点をまたいで被積分関数を積分することはできない。例えば、-π/3<x<2π/3 が、この関数の積分可能な範囲である(そのxの範囲が被積分関数の不定積分の関数が定義されるxの範囲である)。また、2π/3から5π/3までが、この被積分関数のもう一つの積分可能な範囲である(もう1つの不定積分の関数が定義されるxの範囲である)。
〔第1の定義域の不定積分〕
次に、以下のように、変数uを定義し、第1の定義域の不定積分の計算の準備をする。
すなわち、以下の式のように、第1の定義域の不定積分の積分範囲を、被積分関数の分母が0になる点を境界点にした区間にする。


次に、以下の置換積分の計算をします。






(第1の定義域の不定積分おわり)
〔第2の定義域の不定積分〕
次に、以下のように、変数uを定義し、第2の定義域の不定積分の計算の準備をする。
すなわち、以下の式のように、第2の定義域の不定積分の積分範囲を、tan(x/2)が無限大になる点を境界点にした区間にする。

これ以降は、第1の定義域の不定積分を計算した場合と同様にして、式(25)以降の計算を行ない、第2の定義域での以下の不定積分F(x) を得る。

(第2の定義域の不定積分おわり)
〔第3の定義域の不定積分〕
次に、以下のように、変数uを定義し、第3の定義域の不定積分の計算の準備をする。
すなわち、以下の式のように、第3の定義域の不定積分の積分範囲を、tan(x/2)が無限大になる点を境界点にした区間にする。

これ以降は、第1の定義域の不定積分を計算した場合と同様にして、式(25)以降の計算を行ない、第3の定義域での以下の不定積分F(x) を得る。

(第3の定義域の不定積分おわり)
(不定積分の定義域の結合)広義積分の適用について:
第2の定義域の不定積分の関数F(x) と第3の定義域の不定積分の関数F(x) の定義域の境界点(x=π)では、置換積分の媒介変数u=tan(x/2)が無限大になる。その境界点で、両者の不定積分F(x) の極限値がlog|tan(4π/6)|+Cになり、有限な極限値を持つ。そのため、その極限値を、x=πの点での不定積分の値であるとして関数の値F(π) を定義する(広義積分を適用する)。そして、第2の定義域の不定積分F(x) と第3の定義域の不定積分F(x) の定義域をつないで、式(52b)の1つの定義域にし、

そのxの範囲を定義域とする不定積分F(x) を以下の式にする。

(第2の定義域と第3の定義域の不定積分の結合おわり)
【解3】
「積分計算と相性が良い三角関数の積の分数の分解の公式」を用いて、以下のように計算することもできます。

ここで、「積分計算と相性が良い三角関数の積の分数の分解の公式」を適用する。

(解3おわり)
リンク:
高校数学の目次
【問1】
以下の不定積分を求めよ。
【解1】
この問題を、
tan(x/2)=tとする変数tを正しく導入して以下の様に解きます。
(変数tを導入する考え方)
tan(x/2)=t
とする変数tを導入する場合は、
「ここをクリックした参考サイトの様な解き方」
をすると、
x/2=π/2の点で、
tan(x/2)の値が無限大になってしまうので、
その点を含む x の区間では積分できない
という問題があります。
(ここをクリックした先の「広義積分を必要とする積分の例」を参照)
この問題が積分の計算に障害を生じ無いようにするには、
被積分関数の
の分母が0になって、この被積分関数が積分できない場合に合わせて、
その場合が、tan(t/2)の値が無限大になる場合でもあるようにすると良いのです。
すなわち、
以下の様に計算します。

この変数tがπになる点で式5の積分ができない。
そのtの値のときが、
u=tan(t/2)の値が無限大になる場合でもあるように、置換積分するための変数 u を整合すると良いのです。
すなわち、以下の様に計算します。
このように、
変数uによる変数tの制限条件の式8を、被積分関数の積分の制限条件の式6に整合させます。
こうしておいて、以下のように、計算の準備をします。
こうして準備した上で、
以下の積分の計算をします。
(解1おわり)
(補足1)
なお、この積分では、変数変換をして、
被積分関数を、
1/sin(t)の t による積分に変換した上で、
tan(t/2)=u
とする変数 u を導入した計算をしました。
このような形に被積分関数を変換することが、この置換積分のコツです。
なお、式13の形の式は、「三角関数の分数式の変換公式」の公式4の式7や式6の様に、異なる三角関数の式に書き換える事もできます。
(補足1おわり)
(補足2)
この計算で求めた以下の式は公式として覚えておくと便利だと思います。
この形の式は公式として覚えやすいと思います。
なお、この積分は、以下の式で表すこともできます。
この式は公式としては覚えにくいので覚える必要は無いと思います。
また、解がこの式で得られた場合に、その解を上の式のtan()の対数関数に変換して表す必要もないと考えます。
上の2つの式は互いに対等な解であると考えます。
(補足2おわり)
(補足3)
この問題の解の式13で、
正確に不定積分を記述すると:
(1)0<(x/2)+(π/6) <(π/2) での式13
(2)(π/2)<(x/2)+(π/6) <(π) での式13
(3)(π)<(x/2)+(π/6) <(3π/2) での式13
(4)(3π/2)<(x/2)+(π/6) <(2π) での式13
・・・
という、異なる開区間の定義域で定義された無限個の不定積分の集まりの解であると書くのが正確な解の記述です。
(各不定積分の積分定数Cは、不定積分毎に異なります。)
この不定積分を使って
定積分
F(b)-F(a)
を計算する場合は、
各々の不定積分が定義されている開区間をはみだして定積分してはいけません。
異なる不定積分の定義域にまたがって
F(b)-F(a)
を計算してはいけないのです。
積分が無限大まで進んで次に無限大を引き算して再び有限に戻って辻褄があうようにも見えますが、それは見せかけです。無限大から無限大を引き算して0になるという計算をしてはいけないのです。
(なお、不定積分は必ず1つながりに連続な関数になります。不定積分が1つながりに連続で無い点をまたがって関数を定積分しないようにしましょう。)
(補足3おわり)
【重要な注意】
ここで、tan(x/2)=tとする変数tを導入する場合には、tan(x/2)が定義されていない(微分できない)x(例えばx=π,3πなど)を不定積分の定義域から省く必要があります。
そのために、上の解き方のような技巧的な解き方をしました。
いつもそうしなければいけないとなると、tan(x/2)=tとする変数tを自由に導入して置換積分ができなくなります。
しかし、それを改善する手段があります。
(1) tan(x/2)が無限大になってその点のxで積分できないので、不定積分の変数xの定義域を、そのxの点を境界点にしたその境界点以外の左側の区間を第1の不定積分の変数xの定義域にする。また、その境界点以外の右側の区間を第2の不定積分の変数xの定義域にする。そのように、定義域が異なる2つの不定積分の解を求める。
(2) そのように定義域がバラバラな不定積分の解同士が、そのxの境界点で、不定積分の有限な値の極限値があり、そのxの境界点で、第1と第2の不定積分の解が接続できる場合は、そのxの境界点での極限値をその不定積分の関数の値として定義する。それは広義積分と呼ばれている。広義積分をすることを明確にするために、以下の説明文を解答に加える。
「この不定積分の関数F(x)でのcos(x/2)→0となる変数xの極限でのF(x)の極限値を、そのxの値でのF(x)の値と定義する」
そして、xの境界点の左右の区間をつないで一体化して1つの区間にし、その区間を第1と第2の不定積分を合体させた関数F(x) の定義域にする。こうして、元の関数ではxの値が定義されていたが、tan(x/2)=tとする変数tを導入することで潰された変数xの値を、広義積分によってそのxの点での関数F(x)の値を定義することでそのxの点を定義域に復活させる。また、関数F(x) の定義域の区間を拡大する。
【解2】
この関数の積分を、
tan(x/2)=uとする変数uを直接的に導入して以下の様に置換積分して解きます。

先ず、被積分関数の分母が0になる、積分できないxの点を求める。

この値のxの点をまたいで被積分関数を積分することはできない。例えば、-π/3<x<2π/3 が、この関数の積分可能な範囲である(そのxの範囲が被積分関数の不定積分の関数が定義されるxの範囲である)。また、2π/3から5π/3までが、この被積分関数のもう一つの積分可能な範囲である(もう1つの不定積分の関数が定義されるxの範囲である)。
〔第1の定義域の不定積分〕
次に、以下のように、変数uを定義し、第1の定義域の不定積分の計算の準備をする。
すなわち、以下の式のように、第1の定義域の不定積分の積分範囲を、被積分関数の分母が0になる点を境界点にした区間にする。


次に、以下の置換積分の計算をします。






(第1の定義域の不定積分おわり)
〔第2の定義域の不定積分〕
次に、以下のように、変数uを定義し、第2の定義域の不定積分の計算の準備をする。
すなわち、以下の式のように、第2の定義域の不定積分の積分範囲を、tan(x/2)が無限大になる点を境界点にした区間にする。

これ以降は、第1の定義域の不定積分を計算した場合と同様にして、式(25)以降の計算を行ない、第2の定義域での以下の不定積分F(x) を得る。

(第2の定義域の不定積分おわり)
〔第3の定義域の不定積分〕
次に、以下のように、変数uを定義し、第3の定義域の不定積分の計算の準備をする。
すなわち、以下の式のように、第3の定義域の不定積分の積分範囲を、tan(x/2)が無限大になる点を境界点にした区間にする。

これ以降は、第1の定義域の不定積分を計算した場合と同様にして、式(25)以降の計算を行ない、第3の定義域での以下の不定積分F(x) を得る。

(第3の定義域の不定積分おわり)
(不定積分の定義域の結合)広義積分の適用について:
第2の定義域の不定積分の関数F(x) と第3の定義域の不定積分の関数F(x) の定義域の境界点(x=π)では、置換積分の媒介変数u=tan(x/2)が無限大になる。その境界点で、両者の不定積分F(x) の極限値がlog|tan(4π/6)|+Cになり、有限な極限値を持つ。そのため、その極限値を、x=πの点での不定積分の値であるとして関数の値F(π) を定義する(広義積分を適用する)。そして、第2の定義域の不定積分F(x) と第3の定義域の不定積分F(x) の定義域をつないで、式(52b)の1つの定義域にし、

そのxの範囲を定義域とする不定積分F(x) を以下の式にする。

(第2の定義域と第3の定義域の不定積分の結合おわり)
【解3】
「積分計算と相性が良い三角関数の積の分数の分解の公式」を用いて、以下のように計算することもできます。

ここで、「積分計算と相性が良い三角関数の積の分数の分解の公式」を適用する。

(解3おわり)
リンク:
高校数学の目次


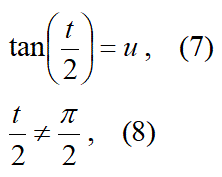






0 件のコメント:
コメントを投稿