これは、ここをクリックした先の問題の解答です。
【問0】(難問)
プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。
(場合1)
プレーヤーが1つのドアを選択した後、
プレーヤーが正解のドアを選んでいてもいなくても必ず、正解ドアを知っている司会のモンティが、プレーヤーがドアを選んだ後に、残りのドアのうち必ずヤギがいる1つのハズレのドアを間違えずに開けてヤギを見せる。
そして、プレーヤーには必ず、最初にプレーヤーが選んだ1つのドアを、こうして正解を知っているモンティが抽出して残した1つドアに変更してもよいと許可するルールである。
プレーヤーはドアを変更すべきだろうか?
(場合2)
プレーヤーが1つのドアを選択した後、選択されたドアに鍵がかけられた。
そうしたらもう1人のプレーヤーが間違えて、ドアを開こうして、鍵がかかっているドアは開かないので、鍵がかかっていない残りの2つのドアのうちの1つを開けてしまった。
その開けられたドアの後ろにはヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
ここでプレーヤーは、最初に選んだドアを、残っている、1つのドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず許可するルールになっていた)
プレーヤーはドアを変更すべきだろうか?
(場合3)
当事者プレーヤーが1つのドアを選択した後、選択されたドアには鍵をかけなかった。
そうしたら他人のプレーヤーが間違えて、ドアを開けてしまった。そのドアは、たまたま当事者プレーヤーが選んだドア以外のドアだった。
その開けられたドアの後ろにはヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
ここで当事者プレーヤーは、最初に選んだドアを、残っている、選ばれていないドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず許可することになっていた)
プレーヤーはドアを変更すべきだろうか?
(1990年9月9日発行、ニュース雑誌 Parade)
【解答方針】
この問題は、モンティ・ホール問題と呼ばれていて、その解答が誤りだとする大論争が起きた問題です。
場合1では、司会者の行動は偶然の行為の結果では無く、司会者が、意識的に、まだ選ばれていない残りのドアのハズレの可能性を低くした点に特徴があります。
この問題は、難しいので、先ず類似の分かり易い問題を解いてみます。
【分かり易しくした問題1】
プレーヤーの前に閉まった10のドアがあって、1つのドアの後ろには景品の新車が、9つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。
(問題1の場合1)
プレーヤーが1つのドアを選択した後、
プレーヤーが正解のドアを選んでいてもいなくても必ず、正解ドアを知っている司会のモンティが、プレーヤーがドアを選んだ後に、残りのドアのうち必ずヤギがいる8つのハズレのドアを間違えずに開けてヤギを見せる。
そして、プレーヤーには必ず、最初にプレーヤーが選んだ1つのドアを、こうして正解を知っているモンティが抽出して残した1つドアに変更してもよいと許可するルールである。
プレーヤーはドアを変更すべきだろうか?
【問題1の場合1の解答】
この問題が出た当初に大論争が起きたのは、おそらくこの問題が、戦略・ゲームの問題として出題され、そのゲームのルールが不明であったためと考えられます。
「正解を知る司会者(元締め)による、ハズレドアBの開示行為が、プレーヤーと勝負している司会者(元締め)を勝たせる戦略として最善の行為であると考えなさい。」という問題であるならば、
とても、以下の説明の様な簡単な答えは出せないと考えます。
しかし、先の問題文の様に、司会者の行動を完全に定義したならば、問題は易しくなったと考えます。
(1)
プレーヤーが選んだドアが正解である確率は、
である。
そして、 プレーヤーが選んだドア以外の9つのドアのうちの1つが正解である確率は、
である。
(2)
一方、正解ドアを知っている司会者がプレーヤーが選んだドア以外の9つのドアのうちから、間違いをせずに、8つのハズレのドアを除去する作業をして1つのドアだけ残すというドアの除去作業を行なう。
この司会者による作業は必ず行なわれ、司会者がこれと違う行為を行なう/又は行なわないという事象は存在しない。
(この司会者の作業の結果はいつも同じ結果のハズレに定まっていて、正解ドアが開かれることは決して無いので、作業(事象)の実行により正解確率の一部が消える条件付き確率問題の事態が発生し無い。)
その司会者の作業は、以下の様にして、プレーヤーが選ばなかった9つのドアのうちに正解のドアがある場合に、その正解のドアがどれであっても残す、正解の抽出作業である。
(2-1)プレーヤーが選ばなかった9つのドアのうちいずれか1つのドアが正解であるならば、その正解であるドアを残し、
(2-2)あるいは、プレーヤーが選んだドア以外の9つのドアが全てハズレであるならば、正解では無い1つのドアのみを残し、それ以外のハズレのドアを明確にして除外する、
注意深く選別する確実な作業を行なう。
その作業の結果は、残された1つのドアが正解である確率は、元の9つのドアの集合全体のうちの1つが正解である確率を引き継ぎ、確率が
である。
(3)
プレーヤーが選んだドアが正解である確率
は、この司会者の操作の結果によって変わらない。
(その理由は、正解ドアを知っている司会者から見て、ドアAの正解確率が変わらないからである。)
実際、このプレーヤーが選択したドアの正解確率(1/10)と、
司会者が残した1つのドアの正解確率
の和は1であるので、以上の計算は誤っていない。
(4)
よって、場合1では、
正解を知っている司会者が開くことが出来る司会者の影響力の圏内で、司会者によって抽出されて残された1つのドアが正解である確率は、
(司会者以外の者から見たら)
司会者が抽出した1つのドアに正解の確率を凝縮したので、
プレーヤに選ばれた1つのドアが正解である確率よりも、
9倍高い正解確率になる。
(場合1の解答おわり)
(なお、司会者から見れば、単に、正解のドアを残しただけであり、どのドアが正解であるかは初めから決まっていて、それは変化しない。また、正解を知っている司会者から見れば、プレーヤーに選ばれた1つのドアに比べて、それ以外の9つのドアの集合内では、ドア数に比例して正解のドアが存在する確率が高いことが分かる。)
(補足)
ここで、(問題0において)司会者がハズレのドアを開いた場合に、残りのドアは、プレーヤーが選んだ1つのドアと司会者が残した1つのドアとの2つのみになる。そのうち1つのドアがハズレで、1つのドアが正解の状況になる。その状況を見て、「未だ開いていない2つのドアは、平等に正解の確率が1/2にリセットされる。」と誤解する人が多いそうです。
そのように誤解する人に対しては、
「正解の確率は、いつでも平等に、未だ開いていない2つのドアに割り振られる原理があるわけではない。「場合1」における司会者の操作の結果の様に、未だ開いていない2つのドアに異なる割合で正解の確率が割り付けられる場合がある。」と返答したい。
《問題0の(場合1):3つのドアの場合において、ハズレである場合に限ってドアBを除去するとき》
先ず、プレーヤーがドアAを選択して、未だ司会者が何もしない場合の状態は以下の樹形図であらわせる。

(ドアBがハズレであることを知る司会者がドアBを除去した場合)
司会者がそういう意図でドアBを除去した場合の、その後のドアAとCの条件付き確率PB(A)と、PB(C)は、以下の樹形図を書いて計算できる。

ドアBが除去される状況になる確率とドアCが除去される状況になる確率は、ともに1/2であるので、
ドアAが正解であってドアBが除去される確率は、
(1/3)(1/2)=1/6になる。
ドアCが正解であってドアBが除去される確率は、
(1/3)・1=1/3になる。
両確率の合計は、1/2である。
その結果の、ドアAとCの条件付き確率PB(A)と、PB(C)は、それらの確率を両確率の合計(=1/2)で割り算することで得られる。その結果は、以下のようになる。
(A)司会者が除去する対象外(影響圏外)のドアAが正解である条件付き確率は、
PB (A)=Pa(A)=1/3
であり確率が変わらない。
(C)司会者がドアBを開いて除去した場合に、司会者が除去する対象だったのに除去しなかった(あるいは正解なので除去できなかった)ドアCが正解である条件付き確率は、
ドアAとは条件が異なり、
PB (C)=2・Pa(C)=2/3になる。
PB(A) +PB(C)=1,
が成り立つ。
ここで注目する点は、ドアBとドアCの集合から正解ドア候補Bを(それがハズレの場合に限って)除去する操作を行なうと、除去したドアBが持っていた正解の確率がドアCの正解の確率に加えられた結果の(ドアBが開かれた後での)ドアCの正解の条件付き確率になることです。
これは、正解ドアを知っている司会者から見れば、ドアBとドアCから、不正解(ハズレ)と分かっているドアを除去することで、正解可能性を絞り込む操作をしたのです。
この操作には、以下の特徴があります。問題1の(場合1)において、この操作を、状況のバラエティに応じて行なうバラエティの各々には、以下の特徴がある。その特徴とは、いつも同じドアBが除去されるわけでは無い(ドアBが正解の場合には除去されない)こと。除去されるドアが状況により変わる、除去ドアが定まらない不定性があるという特徴があります。
(場合1)では、正解ドアを知っている司会者は、除去ドア不定性で特徴付けられた集合のドアの正解確率を(不定性がある)少数のドアに集積させる確率の濃縮・抽出操作を行なうことができます。
それに対して、(場合2)では、正解ドアを知らない者が行なえる操作は、所定のドアを開けてそのドアが偶然にハズレの場合に、残りの全てのドアの正解確率を(見かけ上では)上げる。また、(場合3)では、正解ドアを知らない者が偶然に正解ドアを開けることで、その正解ドアの正解確率を1に上げる操作を行う。
(以上の説明をまとめると)
すなわち、「司会者の操作の影響圏外のドアが正解になる確率は、司会者の行為によって勝手にリセットされるわけではなく、その確率が変わるように見える特別な機構に従って変化する。特に、初めから正解ドアを知っている司会者が見て変わらない状況は、変わらない。」
その「確率が変わるように見える特別な機構」 を、「場合2」と「場合3」で詳しく説明します。
この「場合2」や「場合3」のように明確な手続きに従って、「条件付き確率のみかけの変化」が導き出されるのであり、その手続き無しで勝手に確率が変化すると考えるのは早計だと思います。
(問題1の場合2)
プレーヤーが1つのドアを選択した後、選択されたドアに鍵がかけられた。
そうしたらもう1人のプレーヤーが間違えて、ドアを開こうして、鍵がかかっているドアは開かないので、鍵がかかっていない残りの9つのドアのうちの8つを開けてしまった。
その開けられた8つのドアの後ろには偶然に、全てヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
(そういう場合が偶然発生した場合を条件にする条件付き確率の問題である。)
ここでプレーヤーは、最初に選んだドアを、残っている、1つのドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず行なうルールであった。
また、正解ドアが開けられてしまった場合は、このイベントを中止するルールであった。)
プレーヤーはドアを変更すべきだろうか?
【場合2の解答】
場合2では、正解のドアが開かれてしまう事象以外の事象の後の場合であることを大前提にしている。
そのため、正解のドアが開かれる事象を含む事象の確率は、確率計算の前提から除外して計算しなければならない。
(1) 鍵がかかっているドアが正解の場合:
鍵がかかっているドアが正解の場合には、
残りのドアを8つ開かれても、当然に、全て外れになる。
その場合の確率は、
鍵がかかっているドアが正解である確率であって、
である。
(2) 残りのドア9つのうちの1つが正解の場合:
残りのドア9つのうちの1つが正解の場合であって、
そのうち8つ開かれるドア全てが外れる場合の確率は、
である。
(3) 正解のドアが開かれてしまう場合:
残りのドア9つのうちの1つが正解である場合に、8つ開かれるドアのうちに正解ドアが含まれてしまう確率は、(2)の場合の、8つが全て外れる場合の余事象であるので、
である。
(1)と(2)と(3)の確率を足すと1になるので、以上の計算は誤っていない。
(4)
ここで、この(3)の場合を除外して、正解のドアが開かれてしまう事象以外の事象の後の事象を前提にすると、
(条件付き確率の問題を解くと、)
(4-1)
鍵がかかっているドアが正解の場合の、問題の(正解ドアが開かれ無かった場合の)条件付き確率は、
である。
(4-2)
残ったドアが正解の場合の、問題の(正解ドアが開かれ無かった場合の)条件付き確率は、
である。
よって、場合2では、選ばれたドアが正解である確率と残り1つのドアが正解である確率が等しい。
《問題0の(場合2)3つのドアの場合において、無作為にドアBを開くとき》

ドアBが開かれる事象Bが発生すると、その事象が残りのドアAとCの正解確率に与える影響を定める原理は、以下の様に働くと考えられます。
ドアBが開かれる以前のドアAとBとCの正解確率を、Pa(A) 、Pa(B) 、Pa(C)で定義する。
(1)ドアBを開いてドアBが正解である場合、ドアBが開かれた後のドアAとBとCの正解確率Pb(A) 、Pb(B) 、Pb(C)は、
Pb(B)=1,
Pb(A)=0, Pb(C)=0,
になる。そして、イベントは中止。
(2)ドアBを開いてドアBがハズレである場合の、ドアAとCが正解である条件付き確率Pb(A)とPb(C) は、ドアBかドアCを開く以前の確率Pa(A)とPa(C)と、ドアBかドアCが開かれる確率(1/2)との積を使った以下の式であらわされる。
Pb (A)=(1/2)Pa(A)/((1/2)Pa(A)+(1/2)Pa(C))
Pb (C)=(1/2)Pa(C)/((1/2)Pa(A)+(1/2)Pa(C))
Pb(A) +Pb(C)=1,
で計算できる。
ここで、 ((1/2)Pa(A)+(1/2)Pa(C))で割り算するのは、ドアBがハズレである事象における条件付き確率を求めるためである。
ここで注目する点は、 ドアBがハズレであった事象が発生した前後において、ドアAとドアCの正解の可能性の比が変わらないことです。
Pb(A)=1/2であり、Pb(C)=1/2である。
そのように、「条件付き確率」は、確率を多めに考えるという約束事に従って、開けられず残ったドアの確率が増えたように見せている。
(問題1の場合3)
当事者プレーヤーが1つのドアを選択した後、選択されたドアには鍵をかけなかった。
そうしたら他人のプレーヤーが間違えて、8つのドアを開けてしまった。そのドアは、たまたま当事者プレーヤーが選んだドア以外のドアだった。
しかも、偶然に、その開けられた8つのドア全ての後ろにはヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
(そういう場合が偶然発生した場合を条件にする条件付き確率の問題である。)
ここで当事者プレーヤーは、最初に選んだドアを、残っている、選ばれていないドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず行なうルールであった。
また、正解ドア又は当事者プレーヤーが選んだドアが開けられてしまった場合は、このイベントを中止するルールであった。)
プレーヤーはドアを変更すべきだろうか?
【場合3の解答】
場合3では、正解のドア又は選択されたドアが開かれてしまう事象以外の事象の後の場合であることを大前提にしている。
そのため、正解のドアが開かれる事象又は選択されたドアが開かれる事象を含む事象の確率は、確率計算の前提から除外して計算しなければならない。
(1)
選択されたドアが正解である場合に、そのドアが開けられない確率は、
である。
(2)
当事者プレーヤーに選ばれていないドアが正解である場合に、
選択されたドアが開けられもせず、
かつ、正解のドアが開かれない確率は、
である。
(3-1)
選ばれたドアが正解である場合に、8つ開くドアのうちにその正解ドアが開かれてしまう確率は、(1)の場合の、8つが全て外れる場合の余事象であるので、
である。
(3-2)
残りのドア9つのうちの1つが正解である場合に、8つ開くドアのうちに、正解ドアまたは当事者プレーヤーに選択されたドアが開かれてしまう確率は、(2)の場合の、8つが全て外れる場合の余事象であるので、
である。
(1)と(2)と(3-1)と(3-2)の確率を足すと
になるので、以上の計算は誤っていない。
(4)
ここで、この(3)の場合を除外して、正解ドア又は当事者プレーヤーが選んだドアが開かれてしまう事象以外の事象の後の事象を前提にすると、
(条件付き確率の問題を解くと、)
(4-1)
選択されたドアが正解の場合の、問題の(正解ドアも選択ドアも開かれ無かった場合の)条件付き確率は、
である。
(4-2)
選択されたドア以外の残ったドアが正解の場合の、問題の(正解ドアも選択ドアも開かれ無かった場合の)条件付き確率は、
である。
よって、場合3では、選択されたドアが正解である確率と残り1つのドアが正解である確率が等しい。
(解答おわり)
【問題0の解答】
(場合1)
選択ドアがAの場合において、ドアBが開かれる場合を考える。
ドアBが開かれる以前のドアAとBとCの正解確率を、Pa(A) 、Pa(B) 、Pa(C)で定義する。ドアAが正解の場合にドアBが開かれる確率をPb(A)と定義し、ドアCが正解の場合にドアBが開かれる確率をPb(C)と定義する。
以下の、確率の樹形図が描ける。

ドアBがハズレであることを知る司会者が、プレーヤーが選択したドアAには手を加えない。
(a)ドアAが正解の場合に、ドアCを残しドアBを開いて除去するか、又は、ドアBを残しドアCを開いて除去する。
(b)ドアBが正解の場合に、ドアBを残しドアCを開いて除去し、
(c)ドアCが正解の場合に、ドアCを残しドアBを開いて除去する。
そうする場合に:
ドアBが開かれた条件の下で:
選択されたドアAが正解である確率Pb(A)は、
Pb(A)=(1/2)Pa(A),
である。
残ったドアCが正解である確率Pb(C)は、
Pb(C)=Pa(C),
である。
選択されたドアAが正解である確率Pb(A)の2倍が、残りのドアCが正解である確率Pb(C)になる。
プレーヤに選ばれたドアAが正解である確率よりも、司会者が抽出した残りのドアCが正解である確率が2倍高くなる。
よって、プレーヤーに選択された選択ドアAよりも、開かれなかった残り1つのドア(B又はC)が正解である確率が高い。
(場合2)

ドアBが開かれる以前のドアAとBとCの正解確率を、Pa(A) 、Pa(B) 、Pa(C)で定義する。ドアAが正解の場合にドアBが開かれる確率をPb(A)と定義し、ドアCの場合にドアBが開かれる確率をPb(C)と定義する。ドアBが開かれた条件の下に、ドアAが正解である条件付き確率をPB(A)と定義し、ドアBが開かれた条件の下に、ドアCが正解である条件付き確率をPB(C)と定義する。
(1) ドアBを開いてドアBが正解である場合:
このイベントは中止される。
(2) ドアBを開いてドアBがハズレである場合:
ドアBが開かれた後で、
選択ドアAの正解の条件付き確率PB(A)と、残留ドアCの正解の条件付き確率PB(C)は、以下の式で計算される。

この式の計算結果は、
Pa(A)=Pa(C)であった比が維持され、
プレーヤーに選択された選択ドアAが正解である条件付き確率と残りの残留ドアCが正解である条件付き確率が等しく(1/2)になる。
(場合3)
以下の、確率の樹形図が描ける。

問題1の場合3と同様にして、ドアBが開かれた場合の、
選択されたドアAが正解である確率Pb(A)と、
残りの1つの残留ドアCが正解である確率Pb(C)とは、等しい。
選択ドアAの正解の条件付き確率PB(A)と、残留ドアCの正解の条件付き確率PB(C)は、以下の式で計算される。

この式の計算結果は、
Pa(A)=Pa(C)であった比が維持され、
プレーヤーに選択された選択ドアAが正解である条件付き確率と残りの残留ドアCが正解である条件付き確率が等しく(1/2)になる。
(解答おわり)
リンク:
高校数学の目次
【問0】(難問)
プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。
(場合1)
プレーヤーが1つのドアを選択した後、
プレーヤーが正解のドアを選んでいてもいなくても必ず、正解ドアを知っている司会のモンティが、プレーヤーがドアを選んだ後に、残りのドアのうち必ずヤギがいる1つのハズレのドアを間違えずに開けてヤギを見せる。
そして、プレーヤーには必ず、最初にプレーヤーが選んだ1つのドアを、こうして正解を知っているモンティが抽出して残した1つドアに変更してもよいと許可するルールである。
プレーヤーはドアを変更すべきだろうか?
(場合2)
プレーヤーが1つのドアを選択した後、選択されたドアに鍵がかけられた。
そうしたらもう1人のプレーヤーが間違えて、ドアを開こうして、鍵がかかっているドアは開かないので、鍵がかかっていない残りの2つのドアのうちの1つを開けてしまった。
その開けられたドアの後ろにはヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
ここでプレーヤーは、最初に選んだドアを、残っている、1つのドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず許可するルールになっていた)
プレーヤーはドアを変更すべきだろうか?
(場合3)
当事者プレーヤーが1つのドアを選択した後、選択されたドアには鍵をかけなかった。
そうしたら他人のプレーヤーが間違えて、ドアを開けてしまった。そのドアは、たまたま当事者プレーヤーが選んだドア以外のドアだった。
その開けられたドアの後ろにはヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
ここで当事者プレーヤーは、最初に選んだドアを、残っている、選ばれていないドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず許可することになっていた)
プレーヤーはドアを変更すべきだろうか?
(1990年9月9日発行、ニュース雑誌 Parade)
【解答方針】
この問題は、モンティ・ホール問題と呼ばれていて、その解答が誤りだとする大論争が起きた問題です。
場合1では、司会者の行動は偶然の行為の結果では無く、司会者が、意識的に、まだ選ばれていない残りのドアのハズレの可能性を低くした点に特徴があります。
この問題は、難しいので、先ず類似の分かり易い問題を解いてみます。
【分かり易しくした問題1】
プレーヤーの前に閉まった10のドアがあって、1つのドアの後ろには景品の新車が、9つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。
(問題1の場合1)
プレーヤーが1つのドアを選択した後、
プレーヤーが正解のドアを選んでいてもいなくても必ず、正解ドアを知っている司会のモンティが、プレーヤーがドアを選んだ後に、残りのドアのうち必ずヤギがいる8つのハズレのドアを間違えずに開けてヤギを見せる。
そして、プレーヤーには必ず、最初にプレーヤーが選んだ1つのドアを、こうして正解を知っているモンティが抽出して残した1つドアに変更してもよいと許可するルールである。
プレーヤーはドアを変更すべきだろうか?
【問題1の場合1の解答】
この問題が出た当初に大論争が起きたのは、おそらくこの問題が、戦略・ゲームの問題として出題され、そのゲームのルールが不明であったためと考えられます。
「正解を知る司会者(元締め)による、ハズレドアBの開示行為が、プレーヤーと勝負している司会者(元締め)を勝たせる戦略として最善の行為であると考えなさい。」という問題であるならば、
とても、以下の説明の様な簡単な答えは出せないと考えます。
しかし、先の問題文の様に、司会者の行動を完全に定義したならば、問題は易しくなったと考えます。
(1)
プレーヤーが選んだドアが正解である確率は、
である。
そして、 プレーヤーが選んだドア以外の9つのドアのうちの1つが正解である確率は、
である。
(2)
一方、正解ドアを知っている司会者がプレーヤーが選んだドア以外の9つのドアのうちから、間違いをせずに、8つのハズレのドアを除去する作業をして1つのドアだけ残すというドアの除去作業を行なう。
この司会者による作業は必ず行なわれ、司会者がこれと違う行為を行なう/又は行なわないという事象は存在しない。
(この司会者の作業の結果はいつも同じ結果のハズレに定まっていて、正解ドアが開かれることは決して無いので、作業(事象)の実行により正解確率の一部が消える条件付き確率問題の事態が発生し無い。)
その司会者の作業は、以下の様にして、プレーヤーが選ばなかった9つのドアのうちに正解のドアがある場合に、その正解のドアがどれであっても残す、正解の抽出作業である。
(2-1)プレーヤーが選ばなかった9つのドアのうちいずれか1つのドアが正解であるならば、その正解であるドアを残し、
(2-2)あるいは、プレーヤーが選んだドア以外の9つのドアが全てハズレであるならば、正解では無い1つのドアのみを残し、それ以外のハズレのドアを明確にして除外する、
注意深く選別する確実な作業を行なう。
その作業の結果は、残された1つのドアが正解である確率は、元の9つのドアの集合全体のうちの1つが正解である確率を引き継ぎ、確率が
である。
(3)
プレーヤーが選んだドアが正解である確率
は、この司会者の操作の結果によって変わらない。
(その理由は、正解ドアを知っている司会者から見て、ドアAの正解確率が変わらないからである。)
実際、このプレーヤーが選択したドアの正解確率(1/10)と、
司会者が残した1つのドアの正解確率
の和は1であるので、以上の計算は誤っていない。
(4)
よって、場合1では、
正解を知っている司会者が開くことが出来る司会者の影響力の圏内で、司会者によって抽出されて残された1つのドアが正解である確率は、
(司会者以外の者から見たら)
司会者が抽出した1つのドアに正解の確率を凝縮したので、
プレーヤに選ばれた1つのドアが正解である確率よりも、
9倍高い正解確率になる。
(場合1の解答おわり)
(なお、司会者から見れば、単に、正解のドアを残しただけであり、どのドアが正解であるかは初めから決まっていて、それは変化しない。また、正解を知っている司会者から見れば、プレーヤーに選ばれた1つのドアに比べて、それ以外の9つのドアの集合内では、ドア数に比例して正解のドアが存在する確率が高いことが分かる。)
(補足)
ここで、(問題0において)司会者がハズレのドアを開いた場合に、残りのドアは、プレーヤーが選んだ1つのドアと司会者が残した1つのドアとの2つのみになる。そのうち1つのドアがハズレで、1つのドアが正解の状況になる。その状況を見て、「未だ開いていない2つのドアは、平等に正解の確率が1/2にリセットされる。」と誤解する人が多いそうです。
そのように誤解する人に対しては、
「正解の確率は、いつでも平等に、未だ開いていない2つのドアに割り振られる原理があるわけではない。「場合1」における司会者の操作の結果の様に、未だ開いていない2つのドアに異なる割合で正解の確率が割り付けられる場合がある。」と返答したい。
《問題0の(場合1):3つのドアの場合において、ハズレである場合に限ってドアBを除去するとき》
先ず、プレーヤーがドアAを選択して、未だ司会者が何もしない場合の状態は以下の樹形図であらわせる。

(ドアBがハズレであることを知る司会者がドアBを除去した場合)
司会者がそういう意図でドアBを除去した場合の、その後のドアAとCの条件付き確率PB(A)と、PB(C)は、以下の樹形図を書いて計算できる。

ドアBが除去される状況になる確率とドアCが除去される状況になる確率は、ともに1/2であるので、
ドアAが正解であってドアBが除去される確率は、
(1/3)(1/2)=1/6になる。
ドアCが正解であってドアBが除去される確率は、
(1/3)・1=1/3になる。
両確率の合計は、1/2である。
その結果の、ドアAとCの条件付き確率PB(A)と、PB(C)は、それらの確率を両確率の合計(=1/2)で割り算することで得られる。その結果は、以下のようになる。
(A)司会者が除去する対象外(影響圏外)のドアAが正解である条件付き確率は、
PB (A)=Pa(A)=1/3
であり確率が変わらない。
(C)司会者がドアBを開いて除去した場合に、司会者が除去する対象だったのに除去しなかった(あるいは正解なので除去できなかった)ドアCが正解である条件付き確率は、
ドアAとは条件が異なり、
PB (C)=2・Pa(C)=2/3になる。
PB(A) +PB(C)=1,
が成り立つ。
ここで注目する点は、ドアBとドアCの集合から正解ドア候補Bを(それがハズレの場合に限って)除去する操作を行なうと、除去したドアBが持っていた正解の確率がドアCの正解の確率に加えられた結果の(ドアBが開かれた後での)ドアCの正解の条件付き確率になることです。
これは、正解ドアを知っている司会者から見れば、ドアBとドアCから、不正解(ハズレ)と分かっているドアを除去することで、正解可能性を絞り込む操作をしたのです。
この操作には、以下の特徴があります。問題1の(場合1)において、この操作を、状況のバラエティに応じて行なうバラエティの各々には、以下の特徴がある。その特徴とは、いつも同じドアBが除去されるわけでは無い(ドアBが正解の場合には除去されない)こと。除去されるドアが状況により変わる、除去ドアが定まらない不定性があるという特徴があります。
(場合1)では、正解ドアを知っている司会者は、除去ドア不定性で特徴付けられた集合のドアの正解確率を(不定性がある)少数のドアに集積させる確率の濃縮・抽出操作を行なうことができます。
それに対して、(場合2)では、正解ドアを知らない者が行なえる操作は、所定のドアを開けてそのドアが偶然にハズレの場合に、残りの全てのドアの正解確率を(見かけ上では)上げる。また、(場合3)では、正解ドアを知らない者が偶然に正解ドアを開けることで、その正解ドアの正解確率を1に上げる操作を行う。
(以上の説明をまとめると)
すなわち、「司会者の操作の影響圏外のドアが正解になる確率は、司会者の行為によって勝手にリセットされるわけではなく、その確率が変わるように見える特別な機構に従って変化する。特に、初めから正解ドアを知っている司会者が見て変わらない状況は、変わらない。」
その「確率が変わるように見える特別な機構」 を、「場合2」と「場合3」で詳しく説明します。
この「場合2」や「場合3」のように明確な手続きに従って、「条件付き確率のみかけの変化」が導き出されるのであり、その手続き無しで勝手に確率が変化すると考えるのは早計だと思います。
(問題1の場合2)
プレーヤーが1つのドアを選択した後、選択されたドアに鍵がかけられた。
そうしたらもう1人のプレーヤーが間違えて、ドアを開こうして、鍵がかかっているドアは開かないので、鍵がかかっていない残りの9つのドアのうちの8つを開けてしまった。
その開けられた8つのドアの後ろには偶然に、全てヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
(そういう場合が偶然発生した場合を条件にする条件付き確率の問題である。)
ここでプレーヤーは、最初に選んだドアを、残っている、1つのドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず行なうルールであった。
また、正解ドアが開けられてしまった場合は、このイベントを中止するルールであった。)
プレーヤーはドアを変更すべきだろうか?
【場合2の解答】
場合2では、正解のドアが開かれてしまう事象以外の事象の後の場合であることを大前提にしている。
そのため、正解のドアが開かれる事象を含む事象の確率は、確率計算の前提から除外して計算しなければならない。
(1) 鍵がかかっているドアが正解の場合:
鍵がかかっているドアが正解の場合には、
残りのドアを8つ開かれても、当然に、全て外れになる。
その場合の確率は、
鍵がかかっているドアが正解である確率であって、
である。
(2) 残りのドア9つのうちの1つが正解の場合:
残りのドア9つのうちの1つが正解の場合であって、
そのうち8つ開かれるドア全てが外れる場合の確率は、
である。
(3) 正解のドアが開かれてしまう場合:
残りのドア9つのうちの1つが正解である場合に、8つ開かれるドアのうちに正解ドアが含まれてしまう確率は、(2)の場合の、8つが全て外れる場合の余事象であるので、
である。
(1)と(2)と(3)の確率を足すと1になるので、以上の計算は誤っていない。
(4)
ここで、この(3)の場合を除外して、正解のドアが開かれてしまう事象以外の事象の後の事象を前提にすると、
(条件付き確率の問題を解くと、)
(4-1)
鍵がかかっているドアが正解の場合の、問題の(正解ドアが開かれ無かった場合の)条件付き確率は、
である。
(4-2)
残ったドアが正解の場合の、問題の(正解ドアが開かれ無かった場合の)条件付き確率は、
である。
よって、場合2では、選ばれたドアが正解である確率と残り1つのドアが正解である確率が等しい。
《問題0の(場合2)3つのドアの場合において、無作為にドアBを開くとき》

ドアBが開かれる事象Bが発生すると、その事象が残りのドアAとCの正解確率に与える影響を定める原理は、以下の様に働くと考えられます。
ドアBが開かれる以前のドアAとBとCの正解確率を、Pa(A) 、Pa(B) 、Pa(C)で定義する。
(1)ドアBを開いてドアBが正解である場合、ドアBが開かれた後のドアAとBとCの正解確率Pb(A) 、Pb(B) 、Pb(C)は、
Pb(B)=1,
Pb(A)=0, Pb(C)=0,
になる。そして、イベントは中止。
(2)ドアBを開いてドアBがハズレである場合の、ドアAとCが正解である条件付き確率Pb(A)とPb(C) は、ドアBかドアCを開く以前の確率Pa(A)とPa(C)と、ドアBかドアCが開かれる確率(1/2)との積を使った以下の式であらわされる。
Pb (A)=(1/2)Pa(A)/((1/2)Pa(A)+(1/2)Pa(C))
Pb (C)=(1/2)Pa(C)/((1/2)Pa(A)+(1/2)Pa(C))
Pb(A) +Pb(C)=1,
で計算できる。
ここで、 ((1/2)Pa(A)+(1/2)Pa(C))で割り算するのは、ドアBがハズレである事象における条件付き確率を求めるためである。
ここで注目する点は、 ドアBがハズレであった事象が発生した前後において、ドアAとドアCの正解の可能性の比が変わらないことです。
Pb(A)=1/2であり、Pb(C)=1/2である。
そのように、「条件付き確率」は、確率を多めに考えるという約束事に従って、開けられず残ったドアの確率が増えたように見せている。
(問題1の場合3)
当事者プレーヤーが1つのドアを選択した後、選択されたドアには鍵をかけなかった。
そうしたら他人のプレーヤーが間違えて、8つのドアを開けてしまった。そのドアは、たまたま当事者プレーヤーが選んだドア以外のドアだった。
しかも、偶然に、その開けられた8つのドア全ての後ろにはヤギがいた。
(そういう場合が偶然発生した後の事象を前提にする)
(そういう場合が偶然発生した場合を条件にする条件付き確率の問題である。)
ここで当事者プレーヤーは、最初に選んだドアを、残っている、選ばれていないドアに変更してもよいと言われた。
(これは、このような突発事故が起きた場合には、プレーヤーが正解のドアを選んでいてもいなくても必ず行なうルールであった。
また、正解ドア又は当事者プレーヤーが選んだドアが開けられてしまった場合は、このイベントを中止するルールであった。)
プレーヤーはドアを変更すべきだろうか?
【場合3の解答】
場合3では、正解のドア又は選択されたドアが開かれてしまう事象以外の事象の後の場合であることを大前提にしている。
そのため、正解のドアが開かれる事象又は選択されたドアが開かれる事象を含む事象の確率は、確率計算の前提から除外して計算しなければならない。
(1)
選択されたドアが正解である場合に、そのドアが開けられない確率は、
である。
(2)
当事者プレーヤーに選ばれていないドアが正解である場合に、
選択されたドアが開けられもせず、
かつ、正解のドアが開かれない確率は、
である。
(3-1)
選ばれたドアが正解である場合に、8つ開くドアのうちにその正解ドアが開かれてしまう確率は、(1)の場合の、8つが全て外れる場合の余事象であるので、
である。
(3-2)
残りのドア9つのうちの1つが正解である場合に、8つ開くドアのうちに、正解ドアまたは当事者プレーヤーに選択されたドアが開かれてしまう確率は、(2)の場合の、8つが全て外れる場合の余事象であるので、
である。
(1)と(2)と(3-1)と(3-2)の確率を足すと
になるので、以上の計算は誤っていない。
(4)
ここで、この(3)の場合を除外して、正解ドア又は当事者プレーヤーが選んだドアが開かれてしまう事象以外の事象の後の事象を前提にすると、
(条件付き確率の問題を解くと、)
(4-1)
選択されたドアが正解の場合の、問題の(正解ドアも選択ドアも開かれ無かった場合の)条件付き確率は、
である。
(4-2)
選択されたドア以外の残ったドアが正解の場合の、問題の(正解ドアも選択ドアも開かれ無かった場合の)条件付き確率は、
である。
よって、場合3では、選択されたドアが正解である確率と残り1つのドアが正解である確率が等しい。
(解答おわり)
【問題0の解答】
(場合1)
選択ドアがAの場合において、ドアBが開かれる場合を考える。
ドアBが開かれる以前のドアAとBとCの正解確率を、Pa(A) 、Pa(B) 、Pa(C)で定義する。ドアAが正解の場合にドアBが開かれる確率をPb(A)と定義し、ドアCが正解の場合にドアBが開かれる確率をPb(C)と定義する。
以下の、確率の樹形図が描ける。

ドアBがハズレであることを知る司会者が、プレーヤーが選択したドアAには手を加えない。
(a)ドアAが正解の場合に、ドアCを残しドアBを開いて除去するか、又は、ドアBを残しドアCを開いて除去する。
(b)ドアBが正解の場合に、ドアBを残しドアCを開いて除去し、
(c)ドアCが正解の場合に、ドアCを残しドアBを開いて除去する。
そうする場合に:
ドアBが開かれた条件の下で:
選択されたドアAが正解である確率Pb(A)は、
Pb(A)=(1/2)Pa(A),
である。
残ったドアCが正解である確率Pb(C)は、
Pb(C)=Pa(C),
である。
選択されたドアAが正解である確率Pb(A)の2倍が、残りのドアCが正解である確率Pb(C)になる。
プレーヤに選ばれたドアAが正解である確率よりも、司会者が抽出した残りのドアCが正解である確率が2倍高くなる。
よって、プレーヤーに選択された選択ドアAよりも、開かれなかった残り1つのドア(B又はC)が正解である確率が高い。
(場合2)

ドアBが開かれる以前のドアAとBとCの正解確率を、Pa(A) 、Pa(B) 、Pa(C)で定義する。ドアAが正解の場合にドアBが開かれる確率をPb(A)と定義し、ドアCの場合にドアBが開かれる確率をPb(C)と定義する。ドアBが開かれた条件の下に、ドアAが正解である条件付き確率をPB(A)と定義し、ドアBが開かれた条件の下に、ドアCが正解である条件付き確率をPB(C)と定義する。
(1) ドアBを開いてドアBが正解である場合:
このイベントは中止される。
(2) ドアBを開いてドアBがハズレである場合:
ドアBが開かれた後で、
選択ドアAの正解の条件付き確率PB(A)と、残留ドアCの正解の条件付き確率PB(C)は、以下の式で計算される。

この式の計算結果は、
Pa(A)=Pa(C)であった比が維持され、
プレーヤーに選択された選択ドアAが正解である条件付き確率と残りの残留ドアCが正解である条件付き確率が等しく(1/2)になる。
(場合3)
以下の、確率の樹形図が描ける。

問題1の場合3と同様にして、ドアBが開かれた場合の、
選択されたドアAが正解である確率Pb(A)と、
残りの1つの残留ドアCが正解である確率Pb(C)とは、等しい。
選択ドアAの正解の条件付き確率PB(A)と、残留ドアCの正解の条件付き確率PB(C)は、以下の式で計算される。

この式の計算結果は、
Pa(A)=Pa(C)であった比が維持され、
プレーヤーに選択された選択ドアAが正解である条件付き確率と残りの残留ドアCが正解である条件付き確率が等しく(1/2)になる。
(解答おわり)
リンク:
高校数学の目次
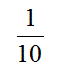











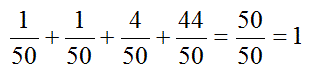


0 件のコメント:
コメントを投稿