外心の高さの式のベクトルでの一番簡単な証明

これは、ここをクリックした先のページの問題の解答です。

【問１】 

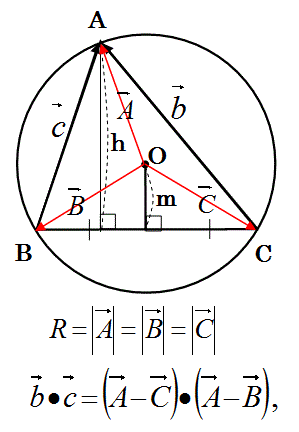
上の三角形において、上のベクトルの内積の式が成り立つことを証明せよ。

【一番簡単な解き方の秘訣】
　（あるベクトルｍとｃとが互いに垂直であるという条件のある図形の問題を解くときは、
（１）それらのベクトルｍとｃを、互いに垂直な単位ベクトルｘとｙの合成であらわして（ただし、ベクトルｘは三角形の所定の辺の方向に平行。ベクトルｙはその辺に垂直な方向を向く）、
（２）そして、ベクトルｍとｃが垂直である条件として内積が０であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。）

　一方で、外心Ｏを原点にした基準ベクトルを使うと、その２つの基準ベクトルの和のベクトルが、その２つの基準ベクトルの差のベクトルに垂直になります（ひし形の対角線の直交の公式）。そのように容易に垂直なベクトルの組を作れるため、上記の場合と同様に、問題が解き易くなります。

【解答（その１）】
先ず、ベクトルｂとｃを、外心から引いたベクトルＡとＢとＣであらわす。

ひし形の対角線の直交の公式により、

が成り立つ。
式ａ１の右辺のベクトルを、その上の式に代入して計算する。

ここでベクトル（Ｂ＋Ｃ）は、上図の様に辺ＢＣに垂直であり、長さが２ｍである。
（証明おわり）

【解答（その２）】
先ず、ベクトルｂとｃを、外心から引いたベクトルＡとＢとＣであらわす。

この式を、大きさＲが等しいベクトルＡとＢとＣの内積であらわし、式を変換する。

（証明おわり）

リンク：
高校数学の目次