これは、ここをクリックした先のページの問題の解答です。
【問1】
上の三角形において、図の角度の条件が成り立つP点の位置座標を求めよ。
ただし、点A,B,Oの位置座標を、A(0,√3)と、B (1,0)と、O(0,0)とする。
(解答方針)
この問題は、正弦定理を使って解くべき問題であって、余弦定理やベクトルの内積を使っては解くべきでない問題です。
ここをクリックした先にあるように正弦定理を使って解くべき問題です。
しかし、複素数平面を使う場合は、この問題を解くことができます。
以下で、複素数平面を使った解答を示します。
【解答】
P点の座標を複素数pであらわして、方程式を立ててpの値を求めます。
ここで、変数sは実数をあらわす。
ここで変数tは実数をあらわす。
以上で得た方程式を以下に整理する。
この方程式7と8からpを消去して実数変数 s と t2 のみを含む式を作る。
この式9の変数sと t2 は実数である。式9の実数部と虚数部が各々0になるので以下の式10と11が成り立つ。
式12で得たsの値を式7に代入して複素数pを求める。
(解答おわり)
この問題は、ベクトルを使って解こうとするととても難しい問題でした(クリックした先のページの第4の解答)が、複素数平面を使って解くと、このように易しく問題が解けるようになりました。
リンク:
高校数学の目次
【問1】
ただし、点A,B,Oの位置座標を、A(0,√3)と、B (1,0)と、O(0,0)とする。
(解答方針)
この問題は、正弦定理を使って解くべき問題であって、余弦定理やベクトルの内積を使っては解くべきでない問題です。
ここをクリックした先にあるように正弦定理を使って解くべき問題です。
しかし、複素数平面を使う場合は、この問題を解くことができます。
以下で、複素数平面を使った解答を示します。
【解答】
P点の座標を複素数pであらわして、方程式を立ててpの値を求めます。
ここで、変数sは実数をあらわす。
ここで変数tは実数をあらわす。
以上で得た方程式を以下に整理する。
この方程式7と8からpを消去して実数変数 s と t2 のみを含む式を作る。
この式9の変数sと t2 は実数である。式9の実数部と虚数部が各々0になるので以下の式10と11が成り立つ。
式12で得たsの値を式7に代入して複素数pを求める。
(解答おわり)
この問題は、ベクトルを使って解こうとするととても難しい問題でした(クリックした先のページの第4の解答)が、複素数平面を使って解くと、このように易しく問題が解けるようになりました。
リンク:
高校数学の目次






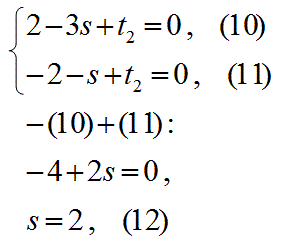

0 件のコメント:
コメントを投稿