以下は、ここをクリックした先の問題の解答です。
【問1】
以下の式1を満たすθの値を求めよ。
【解答】
ここで、変数θを以下の変数αに置き換える。
式2を以下の様に変形する。
ここで sin(α) を変数tに置き換える。
式5を以下の様に変形する。
この式7を解く。
式9の解を単位円を利用して解く。
(解答おわり)
【別解】
この式の両辺を2乗する。
式12を解くために、sin(2θ)をtに置き換える。
この式15によりtが求められた。
単位円を使って式17を満足するθを求める。
式18、式19、式20のθの解のうち、式1を満足する解を選別する。
選別の結果の角度θの解が、以下の式21、式22、式23であらわされた。
(解答おわり)
リンク:
高校数学の目次
【問1】
以下の式1を満たすθの値を求めよ。
【解答】
ここで、変数θを以下の変数αに置き換える。
式2を以下の様に変形する。
ここで sin(α) を変数tに置き換える。
式5を以下の様に変形する。
この式7を解く。
式9の解を単位円を利用して解く。
(解答おわり)
【別解】
この式の両辺を2乗する。
式12を解くために、sin(2θ)をtに置き換える。
この式15によりtが求められた。
単位円を使って式17を満足するθを求める。
式18、式19、式20のθの解のうち、式1を満足する解を選別する。
選別の結果の角度θの解が、以下の式21、式22、式23であらわされた。
(解答おわり)
リンク:
高校数学の目次



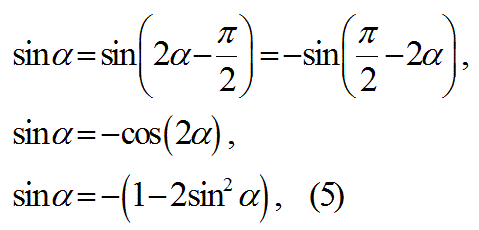


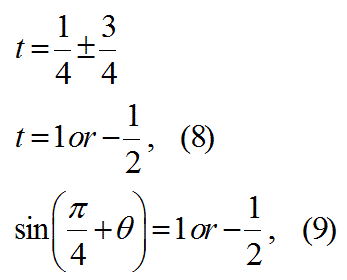









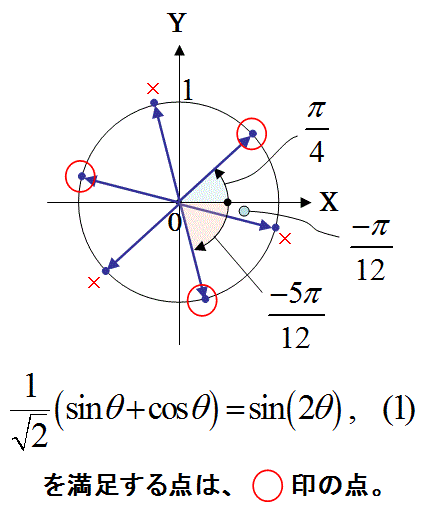

0 件のコメント:
コメントを投稿