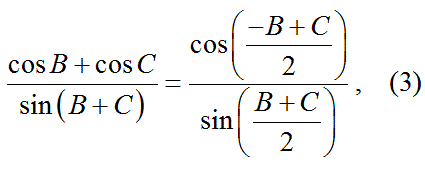分母がｓｉｎ（Ｂ＋Ｃ）の三角関数分数式変換公式

これは、ここをクリックした先のページの問題の解答です。

【公式１】 
分数式の分母が０になる場合を除き、
角度Ｂと角度Ｃに関して、以下の式１：

が成り立つ事を証明せよ。

【証明開始】
先ず、三角関数の和と積の公式で式１の左辺を以下のように変形する。

（証明おわり）

【公式２】 
分数式の分母が０になる場合を除き、
角度Ｂと角度Ｃに関して、以下の式２：

が成り立つ事を証明せよ。

【証明開始】
先ず、三角関数の和と積の公式で式２の左辺を以下のように変形する。

（証明おわり）

【公式３】 
分数式の分母が０になる場合を除き、
角度Ｂと角度Ｃに関して、以下の式３：

が成り立つ事を証明せよ。

【証明開始】
先ず、三角関数の和と積の公式で式３の左辺を以下のように変形する。

以下の式はｃｏｓの和と積の公式から直接導き出すこともできる

（証明おわり）

【公式４】 
分数式の分母が０になる場合を除き、
角度Ｂと角度Ｃに関して、以下の式４：

が成り立つ事を証明せよ。

【証明開始】
先ず、三角関数の和と積の公式で式４の左辺を以下のように変形する。

以下の式はｃｏｓの和と積の公式から直接導き出すこともできる

（証明おわり）

【公式５】 
分数式の分母が０になる場合を除き、
角度Ｂと角度Ｃに関して、以下の式５：

が成り立つ事を証明せよ。

【証明開始】
先ず、三角関数の和と積の公式で式５の左辺を以下のように変形する。

（証明おわり）

【公式６】 
分数式の分母が０になる場合を除き、
公式４の右辺を、以下の式６に変形しなさい。

【証明開始】

（証明おわり）

（補足）
この式６は、以下の様に解釈できる。

（よって、式７が成り立つ）
よって、式６が成り立つ。
以上から、
△ＱＭＮが△ＢＨＣに相似であることによって、
式６が成り立つ。

リンク：
高校数学の目次

三角形の頂角の二等分線の長さに係る証明

これは、ここをクリックした先のページの問題の解答です。

【問１】 

上の三角形において、
三角形ABCの外接円の半径をRとすると、以下の式１：

が成り立つ事を証明せよ。

【証明開始】
先ず、以下の式を三角関数であらわす。

次に、以下の式を三角関数であらわす。

よって：

（証明おわり）

（補足）
　この証明問題は、三角形の頂角の２等分線の長さｍを以下の２つの導き方で得た式を比較する問題でした。
　以下で、第１の導出方法を記載します。

上の図の２つの式を以下の式に変形します。

ここで、以下の関係が成り立ちます。

この関係を式１に代入する。

（公式の第１の導出おわり）

（第２の導出） 
先ず、以下の関係を思い出します。

すなわち、ｂｃ＝２Ｒｈです。

次に、高さｈとｍとの間に以下の関係があります。

高さｈを使うとｍは以下の様に求められます。

（公式の第２の導出おわり）
　これを見ると、この長さｍの２つの導出方法で得た式が等しい事を証明するために必要な計算量は、
それぞれの式を導き出すのに必要な計算量を合計したぐらいの計算量が必要でした。
　そのため、式３というｍの解を求めれば、その解から、その解に等価な式２の解が得られるだろうという予想は、外れている事が分かりました。

リンク：
高校数学の目次

サイコロの目が２種類出る確率

以下は、ここをクリックした先の問題の解答です。

【問題】
１個のサイコロを４回投げる時、出る目の最小値が１、かつ最大値が６である確率を求めよ。

【解答１】
全部の場合の数は
６の４乗＝１２９６通り
あります。

出る目の最小値が１、かつ最大値が６である場合は：
（１）１が先に出て６が後に出る場合
（２）６が先に出て１が後に出る場合
の２つに分けられ、両者の場合の数は同じです。
（１）の場合の数を数えて、２倍すれば、全部の場合の数になります。
１も６も出無い目の出方をＮとします。それは４つの場合があります。
６が出無い目の出方をＴとします。それは５つの場合があります。
どの目が出ても良い目の出方をＡとします。６つの場合があります。
（１）の場合の目の出方は：
この場合を生じる樹形図の、独立した各枝の太さ（場合の数）を数え上げます。

１，６，Ａ，Ａ：　６×６通り＝３６
１，Ｔ，６，Ａ：　５×６通り＝３０
１，Ｔ，Ｔ，６：　５×５通り＝２５
Ｎ，１，６，Ａ：　４×６通り＝２４
Ｎ，１，Ｔ，６：　４×５通り＝２０
Ｎ，Ｎ，１，６：　４×４通り＝１６
合計１５１通り。

全部の場合の数は、この２倍だから、３０２通り。
よって、求める確率Ｐは
Ｐ＝３０２／１２９６＝１５１／６４８
（解答おわり）

【解答２】
以下の様に事象を分離した樹形図を書きます。
下図の縦線は、○印で交差する横線の樹形図の枝を束ねた部分的枝をあらわします。

上図の様に、すぐ分かる確率を、図に書き込みます。
この図から、それ以外の２つの事象の確率も分かるので図に書き込みます。

これらの確率が分かると、
求める事象「どこかで１が出て６も出る事象」の確率Ｐも分かりますので、それを図に書き込みます。

求める事象「どこかで１が出て６も出る事象」の確率Ｐは、以下の様に計算できます。

（解答おわり）

　この問題は、答えが同じ以下の問題を易しくした問題であると考えます。
【問２】
　１個のサイコロを投げて、１の目と６の目が出たらサイコロを投げるのを止めるものとする。その場合に、サイコロの投げ回数が４回以内になる確率を求めよ。

　この問２の様に難しくした問題を解く場合も、
条件が成立してサイコロを投げるのを止めた後でも空投げをする事にして、その空投げは、
「どの目が出ても良い目の出方Ａ」を実行するものとします。この空投げは、６つの場合があります。
この空投げＡを、サイコロを投げるのを止めた後でも実行する事にして問題を易しくして解くと良いと考えます。

リンク：
高校数学の目次