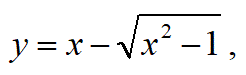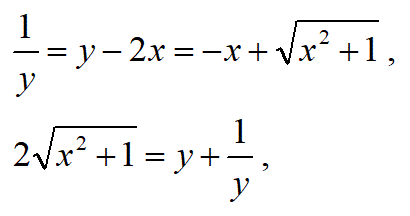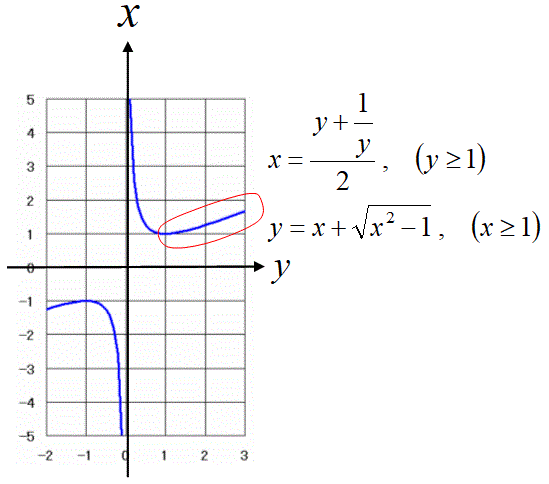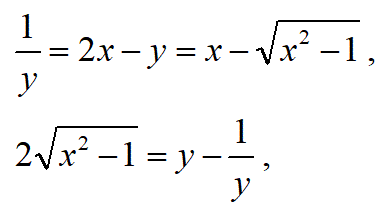これは、ここをクリックした先の問題の解答です。
(解答のための第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
【問1】
下図の複素数平面での三角形の外心Pを表す、以下の形の式を導け

【問1の解答(その1)】(定石の形の解)
図形の定理の、「三角形の高さと外接円の半径の関係の証明(その2)」で考えた図形の定理、すなわち、以下の図で三角形OCHと三角形OEAが相似であるという定理を利用して、外心をあらわす複素数の解を求めます。

三角形OCHと三角形OEAが相似なので、上図のように、
H/C=A/E
の関係があります。
この式に、垂線のベクトルHを表す公式:

を当てはめて外心を表す式を計算します。

(解答おわり)

定石の形の式は、図形の問題の、「三角形の高さと外接円の半径の関係の証明(その2)」で用いた図形の、三角形OCHと三角形OEAが相似である関係を表現した解です。
この2つの三角形が相似という関係を複素数平面で表現すると、
H/C=A/E
でしたが、この様な三角形の相似の関係はベクトルの内積の式で表現する事は困難であり、複素数平面を使う事で初めて表現できるようになりました。
複素数平面の式は、図形の相似の定理と密接な関係にあります。図形で考える思索が複素数平面を使う事で表現できるようになりました。
しかし、一方で、図形の定理を見出すスピードで比較すると、
複素数平面の式の変形操作のスピードよりも図形を思い描く思索のスピードの方が速いです。
大学入試問題の多くは、この定石の形の式を用いると解きやすい問題が出題される場合が多いように感じます。その慣行からすると、第2の形の式(ここをクリックした先の解)よりは、定石の形の式を覚える方が良いように思います。
(定石の形の式の覚え方)
定石の形の式は重要な公式なので覚える必要がありますが、覚えにくい式です。
定石の式の覚え方は、複素数の垂直ベクトルの公式を覚えておいて、毎回、垂直ベクトルの公式を使って定石の式を導き出して使うようにした方が楽だと思います。
リンク:
高校数学の目次
(解答のための第1優先事項)
複素数平面のグラフをあらわす方程式を変換する問題は、複素数の計算をせずに、図形の考察で答えを求めるようにしましょう。すなわち、複素数平面のグラフを表わす複素数の方程式同士を計算でつながないで図形の考察でつなげば何とか問題が解けますのでそれを第1優先にしましょう。
【問1】
下図の複素数平面での三角形の外心Pを表す、以下の形の式を導け

【問1の解答(その1)】(定石の形の解)
図形の定理の、「三角形の高さと外接円の半径の関係の証明(その2)」で考えた図形の定理、すなわち、以下の図で三角形OCHと三角形OEAが相似であるという定理を利用して、外心をあらわす複素数の解を求めます。

H/C=A/E
の関係があります。
この式に、垂線のベクトルHを表す公式:

を当てはめて外心を表す式を計算します。

(解答おわり)

定石の形の式は、図形の問題の、「三角形の高さと外接円の半径の関係の証明(その2)」で用いた図形の、三角形OCHと三角形OEAが相似である関係を表現した解です。
この2つの三角形が相似という関係を複素数平面で表現すると、
H/C=A/E
でしたが、この様な三角形の相似の関係はベクトルの内積の式で表現する事は困難であり、複素数平面を使う事で初めて表現できるようになりました。
複素数平面の式は、図形の相似の定理と密接な関係にあります。図形で考える思索が複素数平面を使う事で表現できるようになりました。
しかし、一方で、図形の定理を見出すスピードで比較すると、
複素数平面の式の変形操作のスピードよりも図形を思い描く思索のスピードの方が速いです。
大学入試問題の多くは、この定石の形の式を用いると解きやすい問題が出題される場合が多いように感じます。その慣行からすると、第2の形の式(ここをクリックした先の解)よりは、定石の形の式を覚える方が良いように思います。
(定石の形の式の覚え方)
定石の形の式は重要な公式なので覚える必要がありますが、覚えにくい式です。
定石の式の覚え方は、複素数の垂直ベクトルの公式を覚えておいて、毎回、垂直ベクトルの公式を使って定石の式を導き出して使うようにした方が楽だと思います。
リンク:
高校数学の目次