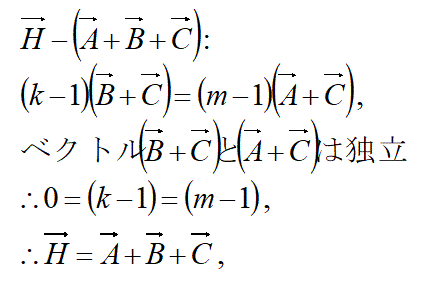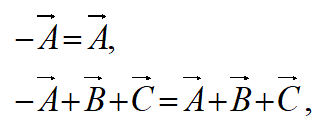勉強しよう数学解答集: 8月 2019

2019年8月3日土曜日

ベクトル方程式で三角形の外心の位置ベクトルを求める

これは、ここをクリックした先の問題の解答です。

大学への数学「ベクトル」編の勉強

【問２】
　頂点Bが原点Oにある三角形ＡBCの外心Pの位置ベクトルPを、位置ベクトルAとCと、その位置ベクトルに垂直なベクトルであらわせ。

【解答】
求める位置ベクトルPは、以下の式１と式２との２つの式であらわせます。この式で係数ｋとmが未知数です。

この式で求めた未知数ｍを位置ベクトルPの式２に代入する。

位置ベクトルPが式5で得られた。
（ベクトルｃｖは、図で上向きのベクトルであるものとする）
（解答おわり）

なお、ベクトルＣv の具体的な式は以下の式で与えられる。ただし、ベクトルC＝(c1,c2)ならば、ベクトルCv＝(-c2,c1)という簡単な式であらわせる。

（図形を平行移動して一般解を求める）
以下で、式５を、点Bを原点から平行移動した図形における外心Pの位置ベクトルの式に変換する。

よって、点Pの座標をあらわす式は、以下の式になる。

（解答おわり）
式８は、位置ベクトルMに、ベクトルBCを90°回転したベクトル（BCv）に平行なベクトルを加えた形で位置ベクトルPを表した式です。

【研究課題】
ここで、ベクトルの分解の公式を使って式８を変換する。

この２つの式を式８に代入する。

（式の変換おわり）

リンク：
高校数学の目次

2019年8月2日金曜日

ベクトル方程式で三角形の垂心の位置ベクトルを求める

これは、ここをクリックした先の問題の解答です。

大学への数学「ベクトル」編の勉強

【問１b】
　三角形ＡOCの垂心Ｄの位置ベクトルを、ベクトルOAとＯCと、それに垂直なベクトルであらわせ。

【解答】
求める位置ベクトルＯＤは、以下の式１と式２との２つの式であらわせます。この式で係数ｋとmが未知数です。

この式で求めた未知数ｋを位置ベクトルｄの式１に代入する。

位置ベクトルｄが式４で得られた。
（ベクトルｃｖは、図で上向きのベクトルであるものとする）
（解答おわり）

リンク：
高校数学の目次

2019年8月1日木曜日

　原点Ｏを中心にした半径Rの円がある。その円上の３点Ａ，Ｂ，Ｃが作る三角形の垂心の位置ベクトルＨを求めよ。

【一番簡単な解き方の秘訣】
　（あるベクトルｍとｃとが互いに垂直であるという条件のある図形の問題を解くときは、
（１）それらのベクトルｍとｃを、互いに垂直な単位ベクトルｘとｙの合成であらわして（ただし、ベクトルｘは、三角形の所定の辺の方向に平行。ベクトルｙはその辺に垂直な方向を向く）、
（２）そして、ベクトルｍとｃが垂直である条件として内積が０であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。）

　一方で、外心Ｏを原点にした基準ベクトルを使うと、その２つの基準ベクトルの和のベクトルが、その２つの基準ベクトルの差のベクトルに垂直になります（ひし形の対角線の直交の公式）。そのように容易に垂直なベクトルの組を作れるため、上記の場合と同様に、問題が解き易くなります。

【解答】

　ここで、上図の式のように、ｋとｍの２つの未知数を用いて、垂心の位置ベクトルＨを表す２通りのベクトルの合成を等しいものと表したベクトル方程式を作ります。（ここで、ひし形の対角線の直交の公式によって、辺に垂直なベクトルが容易に作れる）

垂心のベクトルＨを表す解の式は、点A，Ｂ，Ｃの位置ベクトルに関して対称になると考えられます。
そのため、上の方程式から、位置ベクトルＡ，Ｂ，Ｃに関して対称な式
位置ベクトル（Ａ＋Ｂ＋Ｃ）
を引き算する、方程式の変形を行ないます。

上の方程式の計算によって、未知数ｋとｍの値が定まり、複素数ｈを表す式が求められた。
（解答おわり）

（パラドックスの話）
この問題を以下の様に解析してみます。

先の解答によって、この位置ベクトルHが、位置ベクトルAとBとCの和として表されていました。
その解答を使うと、

という関係が成り立ちます。
この左右の式を合わせるために、とりあえず、

と置いてみます。
そのとき、左右の式の残りの項を比較すると、

となって、残りの項がどうしても一致しません。
式の左右が必ず等しくならなければならないハズなのに、
この矛盾はどうしたことでしょう？？

ここで、ベクトルAとBとCは一次独立では無い。それなのに、一次独立なベクトルの間に成り立つ関係があるとしたところに誤りがあった。
ここで、ベクトルAは以下の式で表せます。