以下は、ここをクリック先の問題の問2の解答です。
【問】
【問】
原点Oを中心にした半径Rの円がある。その円上の3点A,B,Cが作る三角形の垂心の位置ベクトルHを求めよ。
【一番簡単な解き方の秘訣】
(あるベクトルmとcとが互いに垂直であるという条件のある図形の問題を解くときは、
(1)それらのベクトルmとcを、互いに垂直な単位ベクトルxとyの合成であらわして(ただし、ベクトルxは、三角形の所定の辺の方向に平行。ベクトルyはその辺に垂直な方向を向く)、
(2)そして、ベクトルmとcが垂直である条件として内積が0であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。)
一方で、外心Oを原点にした基準ベクトルを使うと、その2つの基準ベクトルの和のベクトルが、その2つの基準ベクトルの差のベクトルに垂直になります(ひし形の対角線の直交の公式)。そのように容易に垂直なベクトルの組を作れるため、上記の場合と同様に、問題が解き易くなります。
【解答】

ここで、上図の式のように、kとmの2つの未知数を用いて、垂心の位置ベクトルHを表す2通りのベクトルの合成を等しいものと表したベクトル方程式を作ります。(ここで、ひし形の対角線の直交の公式によって、辺に垂直なベクトルが容易に作れる)
垂心のベクトルHを表す解の式は、点A,B,Cの位置ベクトルに関して対称になると考えられます。
そのため、上の方程式から、位置ベクトルA,B,Cに関して対称な式
位置ベクトル(A+B+C)
を引き算する、方程式の変形を行ないます。
上の方程式の計算によって、未知数kとmの値が定まり、複素数hを表す式が求められた。
(解答おわり)
(パラドックスの話)
この問題を以下の様に解析してみます。
先の解答によって、この位置ベクトルHが、位置ベクトルAとBとCの和として表されていました。
その解答を使うと、
という関係が成り立ちます。
この左右の式を合わせるために、とりあえず、
と置いてみます。
そのとき、左右の式の残りの項を比較すると、
となって、残りの項がどうしても一致しません。
式の左右が必ず等しくならなければならないハズなのに、
この矛盾はどうしたことでしょう??
ここで、ベクトルAとBとCは一次独立では無い。それなのに、一次独立なベクトルの間に成り立つ関係があるとしたところに誤りがあった。
ここで、ベクトルAは以下の式で表せます。
こうすると、位置ベクトルの表現には、下式のように、いくつものバラエティがあることがわかる。(ベクトルAとBとCが一次独立ではないので、そのようなバラエティがあるのは当然なことです)
例えば、以下の関係が成り立っていたとしたら、どうなるでしょうか。
このとき、
としたら、
という条件を加える事になります。
そうすると、ベクトルAが0ベクトルになるので、ベクトルAの係数が不定になって、
が成り立ってしまいます。
これが、矛盾(パラドックス)の原因でした。
リンク:
高校数学の目次
【一番簡単な解き方の秘訣】
(あるベクトルmとcとが互いに垂直であるという条件のある図形の問題を解くときは、
(1)それらのベクトルmとcを、互いに垂直な単位ベクトルxとyの合成であらわして(ただし、ベクトルxは、三角形の所定の辺の方向に平行。ベクトルyはその辺に垂直な方向を向く)、
(2)そして、ベクトルmとcが垂直である条件として内積が0であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。)
一方で、外心Oを原点にした基準ベクトルを使うと、その2つの基準ベクトルの和のベクトルが、その2つの基準ベクトルの差のベクトルに垂直になります(ひし形の対角線の直交の公式)。そのように容易に垂直なベクトルの組を作れるため、上記の場合と同様に、問題が解き易くなります。
【解答】

ここで、上図の式のように、kとmの2つの未知数を用いて、垂心の位置ベクトルHを表す2通りのベクトルの合成を等しいものと表したベクトル方程式を作ります。(ここで、ひし形の対角線の直交の公式によって、辺に垂直なベクトルが容易に作れる)
垂心のベクトルHを表す解の式は、点A,B,Cの位置ベクトルに関して対称になると考えられます。
そのため、上の方程式から、位置ベクトルA,B,Cに関して対称な式
位置ベクトル(A+B+C)
を引き算する、方程式の変形を行ないます。
(解答おわり)
(パラドックスの話)
この問題を以下の様に解析してみます。
先の解答によって、この位置ベクトルHが、位置ベクトルAとBとCの和として表されていました。
その解答を使うと、
という関係が成り立ちます。
この左右の式を合わせるために、とりあえず、
と置いてみます。
そのとき、左右の式の残りの項を比較すると、
となって、残りの項がどうしても一致しません。
式の左右が必ず等しくならなければならないハズなのに、
この矛盾はどうしたことでしょう??
ここで、ベクトルAとBとCは一次独立では無い。それなのに、一次独立なベクトルの間に成り立つ関係があるとしたところに誤りがあった。
ここで、ベクトルAは以下の式で表せます。
こうすると、位置ベクトルの表現には、下式のように、いくつものバラエティがあることがわかる。(ベクトルAとBとCが一次独立ではないので、そのようなバラエティがあるのは当然なことです)
という条件を加える事になります。
そうすると、ベクトルAが0ベクトルになるので、ベクトルAの係数が不定になって、
が成り立ってしまいます。
これが、矛盾(パラドックス)の原因でした。
リンク:
高校数学の目次
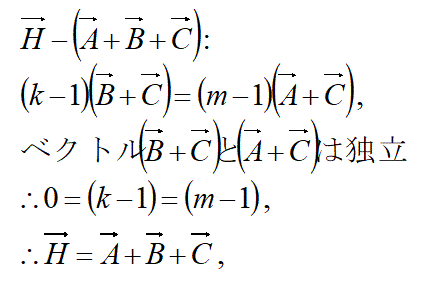









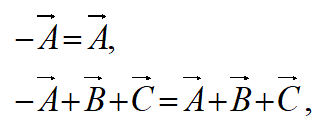
0 件のコメント:
コメントを投稿