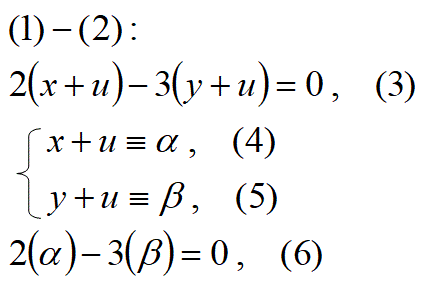以下は、ここをクリックした先の問題の解答です。
【問１】
以下の２つの不定積分AとBを求めよ。
【解答１】
この問題を、正しい部分積分法を使って以下の様に解きます。
先ず、Aの不定積分を部分積分で計算する。
（注意）この式１が正しい部分積分の公式ですが、普通は積分定数C1は省略して書かない。しかし、この問題を解くためには、この公式の積分定数C1を省略できない。
次に、Bの不定積分を部分積分で計算する。
（注意：この式１と式２を組み合わせる事ができるためには、式１と式２で別々に与えられた不定積分AとBを、同じ積分定数を持つ（同じ履歴の）不定積分に調整する必要があります。その調整のためには、式１及び式２は、関数の不定性を与える積分定数C1,C2を残した（省略しない）式にすることが必要です。）
この式１と式２を組み合わせて、不定積分AとBを求める。
（解答１おわり）
【解答１（その２）】
問１を、「純粋な不定積分」を求める問題に修正して、問題を解いてみます。
先ず、Aの不定積分を部分積分で計算する。
次に、Bの不定積分を部分積分で計算する。
この式１と式２を組み合わせて、不定積分AとBを求める。
（解答１（その２）おわり）
不定積分の正しい計算は、このように、純粋な不定積分に戻して考えた場合にも成り立つ計算が正しい計算であると考えます。
（注１）正しい不定積分の式の積分定数C1,C2を省略しないと減点されると言う人もいるようですが、その様な事は（大学の入学試験では）無いと思います。
（注２）「部分積分の式では、両辺に不定積分の式を含むので積分定数Cを省略して良い」という説明がされる事がありますが、それは間違いです。
（補足）
不定積分AやBの加減算を行う場合に、注意しなければならない事は、
というふうに、不定積分は積分定数Cを伴います。
それに関連させて、不定積分同士の引き算の場合：
という事が教えられているようですが、それは間違いだと思います。
同じ式の不定積分同士を引き算して不定積分を無くした際にも、その演算の名残りとして積分定数Cが発生するという教えです。
しかし、その教えでは、解き方があいまいになり解答が劣化しています。
このように、F(x)-F(x)=Cとして解く解き方は、問題を（解答その２に示した）解き方で解く正しい解き方の枠組みを崩す、誤った解き方だと考えます。
不定積分同士の引き算の式：
は、公式と言うよりは、不定積分の計算のあいまいさを表す式と考えます。
この式を使わないで解く解き方、すなわち、F(x)-F(x)=0として解く解き方が、純粋な不定積分の計算に則った正しい解き方であると考えます。
また、F(x)-F(x)=Cとする式は、一旦は、不定積分の計算のあいまいさゆえに、計算が分からない事を表現したものと解釈します。
計算が分からないで、F(x)-F(x)=Cとした式を得ただけと考えます。
その式が得られたら、
0=F(x)-F(x)=C
という正しい等式を成り立たせるために、C＝０にし、不定な値Cを確定させるべきと考えます。
０＝C，かつ，C≠０
とするような矛盾を持ち込むべきでは無いと考えます。
不定積分同士の引き算を、
として解く、以下の計算は間違っていると考えます。
部分積分法の式に積分定数Cを書かずに計算して、
積分定数が無い式３や式４を求めた後でも、
不定積分AやBにはいつも積分定数Cを見え隠れして伴わせ、
式３や式４に唐突に積分定数Cを加える解き方です。
しかし、以上の計算では、計算の途中で（等式を成り立たせる）不定積分の解釈を変えて、その値を変えてしまっているので、間違いであると考えます。
こういう計算をしている場合が多いですが、
そういう解き方は、誤っていると思います。
そういう解き方をするよりも先に、純粋な不定積分を使った場合でも計算が成り立つように計算を進めるべきと思います。
不定積分の正しい計算は、純粋な不定積分に戻して考えた場合にも成り立つ計算が正しい計算であると考えます。
（補足おわり）
【解答２】
先ず、不定積分Aを求める。
次に、不定積分Bを求める。
（解答２おわり）
（補足）
この解答２の積分の計算は、以下の様に、一連の積分計算の最後の式１の右辺に積分定数Ｃを付けるようにする、（推奨される式）を書くことで、
後の式２において唐突に積分定数が現れないようにしても良いと考えます。
上の計算の式１では、その左右の辺が同じでなければならないのですが、
左右に同じ不定積分の式があるので、その不定積分内の積分定数の調整によっては、式１の左辺と右辺が一致するように調整ができません。
そのため、式１では、式１の左辺と右辺を一致させるように調整する積分定数Cを加える必要があります。
（補足おわり）
【解答３】
以下のように一気に部分積分を２回くりかえして問題を解いても良いと思います。
（解答３おわり）
リンク：
高校数学の目次
【問１】
以下の２つの不定積分AとBを求めよ。
【解答１】
この問題を、正しい部分積分法を使って以下の様に解きます。
先ず、Aの不定積分を部分積分で計算する。
次に、Bの不定積分を部分積分で計算する。
この式１と式２を組み合わせて、不定積分AとBを求める。
【解答１（その２）】
問１を、「純粋な不定積分」を求める問題に修正して、問題を解いてみます。
先ず、Aの不定積分を部分積分で計算する。
不定積分の正しい計算は、このように、純粋な不定積分に戻して考えた場合にも成り立つ計算が正しい計算であると考えます。
（注１）正しい不定積分の式の積分定数C1,C2を省略しないと減点されると言う人もいるようですが、その様な事は（大学の入学試験では）無いと思います。
（注２）「部分積分の式では、両辺に不定積分の式を含むので積分定数Cを省略して良い」という説明がされる事がありますが、それは間違いです。
（補足）
不定積分AやBの加減算を行う場合に、注意しなければならない事は、
それに関連させて、不定積分同士の引き算の場合：
同じ式の不定積分同士を引き算して不定積分を無くした際にも、その演算の名残りとして積分定数Cが発生するという教えです。
しかし、その教えでは、解き方があいまいになり解答が劣化しています。
このように、F(x)-F(x)=Cとして解く解き方は、問題を（解答その２に示した）解き方で解く正しい解き方の枠組みを崩す、誤った解き方だと考えます。
不定積分同士の引き算の式：
この式を使わないで解く解き方、すなわち、F(x)-F(x)=0として解く解き方が、純粋な不定積分の計算に則った正しい解き方であると考えます。
また、F(x)-F(x)=Cとする式は、一旦は、不定積分の計算のあいまいさゆえに、計算が分からない事を表現したものと解釈します。
計算が分からないで、F(x)-F(x)=Cとした式を得ただけと考えます。
その式が得られたら、
0=F(x)-F(x)=C
という正しい等式を成り立たせるために、C＝０にし、不定な値Cを確定させるべきと考えます。
０＝C，かつ，C≠０
とするような矛盾を持ち込むべきでは無いと考えます。
不定積分同士の引き算を、
積分定数が無い式３や式４を求めた後でも、
不定積分AやBにはいつも積分定数Cを見え隠れして伴わせ、
式３や式４に唐突に積分定数Cを加える解き方です。
しかし、以上の計算では、計算の途中で（等式を成り立たせる）不定積分の解釈を変えて、その値を変えてしまっているので、間違いであると考えます。
こういう計算をしている場合が多いですが、
そういう解き方は、誤っていると思います。
そういう解き方をするよりも先に、純粋な不定積分を使った場合でも計算が成り立つように計算を進めるべきと思います。
不定積分の正しい計算は、純粋な不定積分に戻して考えた場合にも成り立つ計算が正しい計算であると考えます。
（補足おわり）
【解答２】
先ず、不定積分Aを求める。
（補足）
この解答２の積分の計算は、以下の様に、一連の積分計算の最後の式１の右辺に積分定数Ｃを付けるようにする、（推奨される式）を書くことで、
後の式２において唐突に積分定数が現れないようにしても良いと考えます。
左右に同じ不定積分の式があるので、その不定積分内の積分定数の調整によっては、式１の左辺と右辺が一致するように調整ができません。
そのため、式１では、式１の左辺と右辺を一致させるように調整する積分定数Cを加える必要があります。
（補足おわり）
【解答３】
以下のように一気に部分積分を２回くりかえして問題を解いても良いと思います。
（解答３おわり）
リンク：
高校数学の目次
