以下は、ここをクリックした先の問題の解答です。
(補足)
一次不定方程式の正しい解き方は、ここをクリックした先のサイトにあるように:
1.先ず整数解を1つ求める。
2.もとの方程式と引き算する。
3.一般解を求める。
という計算方法が一番すぐれた解法だと考えます。
【問1】
以下の様に式を書いて、数値をユークリッドの互除法で引き算して行き、最初の数値を文字aとbで表して、ユークリッドの互除法の計算式をaとbの式で表す。

以上の計算で1つの解の式2が得られた。
この1つの解の式2を、元の式1から引き算する。
(1)-(2)
この式3を満足する一般解は、整数mを導入して以下の式であらわせる。
この式を整理する。
(解答1おわり)
【解答2】
以下の解き方の方が覚え易いかもしれない。
式1が求める式である。
先ず、以下の式E7と式E8が成り立つことが分かる。
以上の計算で、解答1と同じく、1つの解の式2が得られた。
次に、この1つの解の式2を、元の式1から引き算します。
(1)-(2)
この式3を満足する一般解を、整数mを導入して以下の式であらわす。
この式を整理する。
(解答2おわり)
【問2】
以下の不定方程式の整数解をすべて求めよ。
【解答】
先ずは、19で割り切れるかを確認する。
2432/19=128,
703/19=37,
割り切れたので、式1を以下の式2に変形する。
次に、ユークリッドの互除法に近い以下の方法で式の計算をして解の1つを求める。
この式を整理する。
(解答おわり)
【問3】
以下の不定方程式の整数解をすべて求めよ。
【解答】
uを予め与えられた整数と考えて、
式1の不定方程式の解を1つだけ求める。
この1つの解の式2を式1から引き算する。
この式の引き算をすると、不定方程式の変数の数が減った。
この不定方程式6の一般解を、整数mを導入して求める。
この式7と8を式4と5に代入して整理する。
(解答おわり)
【問4】
以下の不定方程式の整数解をすべて求めよ。
【解答1】
以下の様に、順次に解を求めていく。
先ず、以下の様にして、xとyの解のバラエティを与える整数mの式を求めます。
次に、以下の様にして、xとyとuの解のバラエティを与える整数sの式を1つ求めます。
(この解は解の全てでは無いが、これで良いです)
これに、整数mの式を加えます。
(解答1おわり)
【解答2】
次に、この不定方程式の解を1つだけ求めます。
次に、この1つの解の式を、元の式1から引き算します。
この式の引き算をすると、不定方程式の変数の数が減りました。
次に、この(x-s)と(y+s)との不定方程式を解きます。
この解と式2とで解があらわせます。
(解答2おわり)
この解答2は、不定方程式の1つの解の式3だけ求めて、それが、全体の解を求める鍵になっています。解答2では、1つの解の式3だけ求めれば良い事の理由が明確に分かるので優れた解き方です。
【問5】
以下の不定方程式の整数解をすべて求めよ。
【解答1】
先ず、不定方程式1の1つの解を求める。
(この解の式2は解の全てでは無いが、これで良いです)
(A)次に、以下の様にして、xとyの解のバラエティを与える整数mの式を求めます。
先ず、以下の整数aとbの不定方程式を解きます。
(B)次に、以下の様にして、xとyとzの解のバラエティを与える整数sの式を1つ求める。
すなわち、以下の整数cとdとeの不定方程式の解の1つを求める。
ここで、整数sに比例する以下の解があります。
(この解は解の全てでは無いが、これで良いです)
(解答1おわり)
【解答2】
以下の様に解く方法の方が、解答1よりも優れています。
先ず、不定方程式1の解を1つだけ求める。
この1つの解の式2を式1から引き算する。
次に、この不定方程式6の解を1つだけ求めます。
整数sを導入して、1つの解を求めました。
次に、この1つの解の式9を式8から引き算します。
この式の引き算をすると、不定方程式の変数の数が減った。
この不定方程式10を、整数mを導入して解く。
以上で得た解を以下で整理する。
(解答2おわり)
この解答2は、不定方程式の1つの解の式2や1つの解の式9だけを求めることが、全体の解を求める鍵になっていること、の理由が明確に分かるので、優れた解き方です。
リンク:
高校数学の目次
(補足)
一次不定方程式の正しい解き方は、ここをクリックした先のサイトにあるように:
1.先ず整数解を1つ求める。
2.もとの方程式と引き算する。
3.一般解を求める。
という計算方法が一番すぐれた解法だと考えます。
【問1】
以下の不定方程式の整数解をすべて求めよ。
【解答1】以下の様に式を書いて、数値をユークリッドの互除法で引き算して行き、最初の数値を文字aとbで表して、ユークリッドの互除法の計算式をaとbの式で表す。

以上の計算で1つの解の式2が得られた。
この1つの解の式2を、元の式1から引き算する。
(1)-(2)
この式3を満足する一般解は、整数mを導入して以下の式であらわせる。
この式を整理する。
(解答1おわり)
【解答2】
以下の解き方の方が覚え易いかもしれない。
式1が求める式である。
先ず、以下の式E7と式E8が成り立つことが分かる。
以上の計算で、解答1と同じく、1つの解の式2が得られた。
次に、この1つの解の式2を、元の式1から引き算します。
(1)-(2)
この式3を満足する一般解を、整数mを導入して以下の式であらわす。
この式を整理する。
(解答2おわり)
【問2】
以下の不定方程式の整数解をすべて求めよ。
【解答】
先ずは、19で割り切れるかを確認する。
2432/19=128,
703/19=37,
割り切れたので、式1を以下の式2に変形する。
次に、ユークリッドの互除法に近い以下の方法で式の計算をして解の1つを求める。
以上の計算で1つの解の式7が得られた。
この1つの解の式7を、元の式1から引き算する。
この式8を満足する一般解を、整数mを導入して以下の式であらわす。この1つの解の式7を、元の式1から引き算する。
この式を整理する。
(解答おわり)
【問3】
以下の不定方程式の整数解をすべて求めよ。
【解答】
uを予め与えられた整数と考えて、
式1の不定方程式の解を1つだけ求める。
この1つの解の式2を式1から引き算する。
この式の引き算をすると、不定方程式の変数の数が減った。
この不定方程式6の一般解を、整数mを導入して求める。
この式7と8を式4と5に代入して整理する。
(解答おわり)
【問4】
以下の不定方程式の整数解をすべて求めよ。
【解答1】
以下の様に、順次に解を求めていく。
先ず、以下の様にして、xとyの解のバラエティを与える整数mの式を求めます。
次に、以下の様にして、xとyとuの解のバラエティを与える整数sの式を1つ求めます。
(この解は解の全てでは無いが、これで良いです)
これに、整数mの式を加えます。
(解答1おわり)
【解答2】
次に、この不定方程式の解を1つだけ求めます。
次に、この1つの解の式を、元の式1から引き算します。
この式の引き算をすると、不定方程式の変数の数が減りました。
次に、この(x-s)と(y+s)との不定方程式を解きます。
この解と式2とで解があらわせます。
(解答2おわり)
この解答2は、不定方程式の1つの解の式3だけ求めて、それが、全体の解を求める鍵になっています。解答2では、1つの解の式3だけ求めれば良い事の理由が明確に分かるので優れた解き方です。
【問5】
以下の不定方程式の整数解をすべて求めよ。
【解答1】
先ず、不定方程式1の1つの解を求める。
(この解の式2は解の全てでは無いが、これで良いです)
(A)次に、以下の様にして、xとyの解のバラエティを与える整数mの式を求めます。
先ず、以下の整数aとbの不定方程式を解きます。
(B)次に、以下の様にして、xとyとzの解のバラエティを与える整数sの式を1つ求める。
すなわち、以下の整数cとdとeの不定方程式の解の1つを求める。
ここで、整数sに比例する以下の解があります。
(この解は解の全てでは無いが、これで良いです)
(解答1おわり)
【解答2】
以下の様に解く方法の方が、解答1よりも優れています。
先ず、不定方程式1の解を1つだけ求める。
この1つの解の式2を式1から引き算する。
次に、この不定方程式6の解を1つだけ求めます。
整数sを導入して、1つの解を求めました。
次に、この1つの解の式9を式8から引き算します。
この式の引き算をすると、不定方程式の変数の数が減った。
この不定方程式10を、整数mを導入して解く。
以上で得た解を以下で整理する。
(解答2おわり)
この解答2は、不定方程式の1つの解の式2や1つの解の式9だけを求めることが、全体の解を求める鍵になっていること、の理由が明確に分かるので、優れた解き方です。
リンク:
高校数学の目次














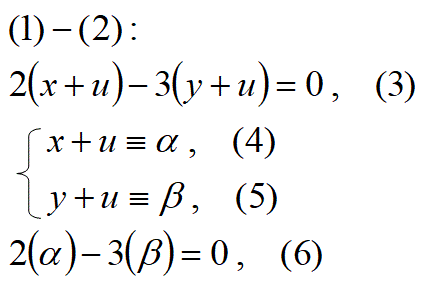
























0 件のコメント:
コメントを投稿