以下は、ここをクリックした先の問題の解答です。
【問題1】
以下の方程式が異なる実数解を2つだけ持つような定数aの値の範囲を求めよ。
【解答1】(定数分離で解く)
式1を以下の様に変形する。
式2の様に、定数aを表す関数f(x)の式を求める。
この関数f(x)のグラフの形を調べる。
以上の結果から、関数f(x)の形を表す増減表を書く。
この増減表から、関数f(x)=aの方程式が異なる実数解を2つだけ持つ定数aの値の範囲は、以下の式であらわせる。
(解答1おわり)
【解答2】
定数分離法を使わないで解くと、例えば、以下の様に解くことになります。
異なる実数解を2つだけ持つには:
(A) a>0 の場合は、
グラフがいったんx軸に接する形になる場合に限る。
(B)a<0の場合は、
グラフの傾きが0になるx=βの点で、g(β)<0となる場合に限る。
(C)a=0 の場合は、
となるので、異なる実数解を2つ持つ。 (解1)
g(x)のグラフが上に凸か下に凸か、凹凸混在かを調べるため、g(x)を2度微分する。
(B) a<0の場合は:
g''(x)>0
になるので、
g(x)のグラフが下に凸になる。
(A) a>0の場合は:
xが十分小さいときは、
g''(x)>0 になるので、グラフが下に凸。
xが十分大きいときは、
g''(x)<0 になるので、グラフが上に凸。
以下で、aの各場合を考察する。
(B) a<0 の場合:
g(x)の最小値は、
となる点x=βである。
その点x=βで、
が成り立つならば、
異なる実数の解を2つだけ持つ。
(4)を(5)に代入:
式7と式4を連立することで解が得られる。
a<0なので、式4より、
式7と式8より、
で、
g'(β)のグラフの形を調べる。a<0なので、
式9により、g'(β)のグラフの傾きが正であるので、
g'(β)が、
の範囲に解を持つためには、
が成り立つことが必要である。
a<0なので、式11は成り立っている。
式10から、
となる。
この式12は、式4と式7を成り立たせる必要条件である。
逆に、式12が成り立てば、式10と式11が成り立つので式7が成り立ち、式4が成り立つので、式12は、式4と式7を成り立たせる必要十分条件である。
よって、式12は、解の1つである。(解2)
(A) a>0 の場合:
であり、また、
xが十分小さいときは、グラフが下に凸であり、
xが十分大きいときは、グラフが上に凸であり、
そして、
である。
そのため、
との、式13と式14が同時に成り立つxの値の点で、
グラフの凸部分がx軸に接することになり、
関数g(x)が異なる実数の解を2つだけ持つ。
(A1) x=1の場合:
式14により、
(解3)
(A2) x=-2の場合:
式14により、
この式は、a>0の場合に成り立たないので不適。
以上の、解1、解2、解3を合わせて、
(解答2おわり)
解答1と解答2を比べてみると、
この種の問題は定数分離で解く方が良いと分かると思います。
【問題1】
以下の方程式が異なる実数解を2つだけ持つような定数aの値の範囲を求めよ。
【解答1】(定数分離で解く)
式1を以下の様に変形する。
式2の様に、定数aを表す関数f(x)の式を求める。
この関数f(x)のグラフの形を調べる。
以上の結果から、関数f(x)の形を表す増減表を書く。
この増減表から、関数f(x)=aの方程式が異なる実数解を2つだけ持つ定数aの値の範囲は、以下の式であらわせる。
(解答1おわり)
【解答2】
定数分離法を使わないで解くと、例えば、以下の様に解くことになります。
異なる実数解を2つだけ持つには:
(A) a>0 の場合は、
グラフがいったんx軸に接する形になる場合に限る。
(B)a<0の場合は、
グラフの傾きが0になるx=βの点で、g(β)<0となる場合に限る。
(C)a=0 の場合は、
となるので、異なる実数解を2つ持つ。 (解1)
g(x)のグラフが上に凸か下に凸か、凹凸混在かを調べるため、g(x)を2度微分する。
(B) a<0の場合は:
g''(x)>0
になるので、
g(x)のグラフが下に凸になる。
(A) a>0の場合は:
xが十分小さいときは、
g''(x)>0 になるので、グラフが下に凸。
xが十分大きいときは、
g''(x)<0 になるので、グラフが上に凸。
以下で、aの各場合を考察する。
(B) a<0 の場合:
g(x)の最小値は、
となる点x=βである。
その点x=βで、
が成り立つならば、
異なる実数の解を2つだけ持つ。
(4)を(5)に代入:
式7と式4を連立することで解が得られる。
a<0なので、式4より、
式7と式8より、
で、
g'(β)のグラフの形を調べる。a<0なので、
式9により、g'(β)のグラフの傾きが正であるので、
g'(β)が、
の範囲に解を持つためには、
が成り立つことが必要である。
a<0なので、式11は成り立っている。
式10から、
となる。
この式12は、式4と式7を成り立たせる必要条件である。
逆に、式12が成り立てば、式10と式11が成り立つので式7が成り立ち、式4が成り立つので、式12は、式4と式7を成り立たせる必要十分条件である。
よって、式12は、解の1つである。(解2)
(A) a>0 の場合:
であり、また、
xが十分小さいときは、グラフが下に凸であり、
xが十分大きいときは、グラフが上に凸であり、
そして、
である。
そのため、
との、式13と式14が同時に成り立つxの値の点で、
グラフの凸部分がx軸に接することになり、
関数g(x)が異なる実数の解を2つだけ持つ。
(A1) x=1の場合:
式14により、
(解3)
(A2) x=-2の場合:
式14により、
この式は、a>0の場合に成り立たないので不適。
以上の、解1、解2、解3を合わせて、
(解答2おわり)
解答1と解答2を比べてみると、
この種の問題は定数分離で解く方が良いと分かると思います。
リンク:
高校数学の目次























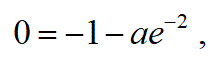

0 件のコメント:
コメントを投稿