この解答は、ここをクリックした先にある問題の解答です。
【問1】
以下の図形のtanθを求めよ。
(注意)この問題は、ラングレーの問題と呼ばれている有名な問題で、難問です。
当ブログでは、三角関数の問題として解きました。
この問題は難問ですので、
三角関数の展開にも、解き方の方向に迷う難しさがあります。
【解答1】
先ず、図形に、すぐわかる角度、長さを全部書きこんで、問題を見通し良くします。

角度を書いたら、二等辺三角形がみつかりました。
さらに、わかる角度、長さを図形に書きこみます。
これで、tanθを計算する情報がそろいました。
 (1)
(1)
この式1の分母は変形できないと考えますので、
分子だけ、変形する計算をすることにします。
ここで分母にあらわれている角度50°を別の角度であらわせるかを考えます。
ここで、右の項にあらわれている角度20°を別な角度であらわすことができるか考えます。
式1の分子が簡単になりましたので、
次に、式1からtanθを計算します。
(解答おわり)
(補足)
上の解答の最後の部分の計算は、
「三角関数の単純化パターンの公式」
に従って、以下のように計算することもできます。

(補足おわり)
【解答2】
以下の図の頂点Cの角度θのtanθを求める問題にして問題を解く。

先ず三角形OABの外接円を書いて、外接円の中心から補助線と角度を図形に書きこんで、問題を解く助けにする。

次に三角形OBCの外接円を書いて、外接円の中心から補助線と角度を図形に書きこんで、問題を解く助けにする。

以下の図のベクトルACのX方向の長さとY方向の長さを計算して、それから線分ACとDCのなす角度を表す方程式を作る。

以下のように、線分OBの中点から見た、左側の点Aと、右側の点Cの各々のX方向の長さとY方向の長さを計算する。

ベクトルACのY方向の長さとX方向の長さを計算する。

線分ACとDCのなす角度を表す方程式を作り、それを解いて角θを求める。


ここで、sin70°の変換公式(群)を使って式を変形する。


こうして、求める角度θが求められた。
(解答おわり)
(補足1)
この問題を解くためには、角度20度や角度70度の三角関数の式の公式群「sin70°の変換公式 」を使うことが必須だった。その公式群によって、計算をどちらの方向に進めたら良いかの計算の見通しがついた。
(補足2)
この公式が、三角関数の式を単純化する計算の見通しを良くするために必要であるのは、複素数平面を使って問題を解く場合も同じである。すなわち、以下の公式が、計算を進めるために必要である。

リンク:
ラングレーの問題って?
高校数学の目次
【問1】
以下の図形のtanθを求めよ。
(注意)この問題は、ラングレーの問題と呼ばれている有名な問題で、難問です。
当ブログでは、三角関数の問題として解きました。
この問題は難問ですので、
三角関数の展開にも、解き方の方向に迷う難しさがあります。
【解答1】
先ず、図形に、すぐわかる角度、長さを全部書きこんで、問題を見通し良くします。

角度を書いたら、二等辺三角形がみつかりました。
さらに、わかる角度、長さを図形に書きこみます。
これで、tanθを計算する情報がそろいました。
 (1)
(1)この式1の分母は変形できないと考えますので、
分子だけ、変形する計算をすることにします。
ここで分母にあらわれている角度50°を別の角度であらわせるかを考えます。
ここで、右の項にあらわれている角度20°を別な角度であらわすことができるか考えます。
式1の分子が簡単になりましたので、
次に、式1からtanθを計算します。
(解答おわり)
(補足)
上の解答の最後の部分の計算は、
「三角関数の単純化パターンの公式」
に従って、以下のように計算することもできます。

(補足おわり)
【解答2】
以下の図の頂点Cの角度θのtanθを求める問題にして問題を解く。

先ず三角形OABの外接円を書いて、外接円の中心から補助線と角度を図形に書きこんで、問題を解く助けにする。

次に三角形OBCの外接円を書いて、外接円の中心から補助線と角度を図形に書きこんで、問題を解く助けにする。

以下の図のベクトルACのX方向の長さとY方向の長さを計算して、それから線分ACとDCのなす角度を表す方程式を作る。

以下のように、線分OBの中点から見た、左側の点Aと、右側の点Cの各々のX方向の長さとY方向の長さを計算する。

ベクトルACのY方向の長さとX方向の長さを計算する。

線分ACとDCのなす角度を表す方程式を作り、それを解いて角θを求める。


ここで、sin70°の変換公式(群)を使って式を変形する。


こうして、求める角度θが求められた。
(解答おわり)
(補足1)
この問題を解くためには、角度20度や角度70度の三角関数の式の公式群「sin70°の変換公式 」を使うことが必須だった。その公式群によって、計算をどちらの方向に進めたら良いかの計算の見通しがついた。
(補足2)
この公式が、三角関数の式を単純化する計算の見通しを良くするために必要であるのは、複素数平面を使って問題を解く場合も同じである。すなわち、以下の公式が、計算を進めるために必要である。

リンク:
ラングレーの問題って?
高校数学の目次
























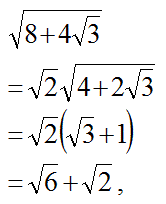

 (7)
(7)





 (9)
(9)