この解答の元の問題はここをクリックした先のページにあります。
〔ページ内リンク〕
▷二重根号の外し方(方法1)
▷二重根号の外し方(方法2)
▷二重根号が外せない場合
▷簡易な計算方法
▷簡易公式2
▷二重根号の外し方(方法3)
▷二重根号の外し方(方法4)
【問】 以下の式の二重根号を外せ。
【注意】二重根号が外せない場合については後に説明しますので、先ずは、以下の、二重根号を外せる場合の説明を読んで下さい。
【二重根号の外し方(方法1)】
先ず、
と変形し、その右側の項の形にします。右側の項を、
と仮定した数xとaを求めます。
(以下の計算方針では、√3という数を含んでいない数(x)と(a)を使って表わせる場合の解だけを求める計算をします。
√3を(x)か(a)が含まざるを得なかったら、そこで計算を終わりにする覚悟をして、以下の計算をします)
この式の両辺を二乗します。
と、
がなりたつと考えることができます。
2つ目の式を更に簡単にすると、

1=a2x (2)
になります。
(2)より、
(3)を(1)に代入します。
この式から、
この式4を因数分解して解くと:
(a-1)(a-3)=0
a=1 or 3
a=1の場合を(3)に代入すると、
x=1
よって、
です。
(a=3の場合も:x=1/9になって、それを代入すると同じ答えになります)
そのため、
になりました。
【二重根号の外し方(方法2)】
二重根号を外すもう1つの方法を説明します。
(原理について)
という形をしている2重根号は、以下の条件が成り立つ場合に外すことができます。
a=x+y (5)
b=x・y (6)
となるxとyを探します。
そのxとyがあれば、
 (7)
(7)
です。

となるからです。
式5と6の解のx、yを求めるということは、
x2-a・x+b=0 (8)
の解x、yを求めることと同じです。この式8は、式4と同じ式になります。
(具体例について)
具体的な今回の以下の問題の場合は、以下のようにして解きます。
の場合は、
と変形します。
この様に、ルートの中の式は、ルートの2倍の項を含む式に変形して、答えを求めます。
を解く場合は、
(x2-4・x+3=0 (式4)を解くのと同じですが)
x+y= a=4=3+1
xy= b=3=3・1
がなりたちますので
x=3
y=1
が見つかりました。
です。
そのため、
です。
【二重根号が外せない場合】
という形をしている2重根号は、
|a2-4b|の平方根の式が、その平方根記号を外せる場合に2重根号を外すことができます。
(1) 先ず、
a2-4b≧0の場合で、その平方根の式が、その平方根記号を外せる場合に平方根を外すことができます。
a2-4b=(x+y)2-4xy=(x-y)2
だからです。
すなわち、
(a2-4b)の平方根=|x-y|
であり、一方、
a=x+y
だったので、この2つの式からxとyが求められるからです。
(2) 次に、√(a(√b)+2b)を考えることで、結局、
4b-a2≧0の場合で、その平方根の式が、その平方根記号を外せる場合も、2重根号を外すことができます。
しかし、|a2-4b|の平方根の式から平方根記号が外せ無いときは、先の式の二重根号を外すことができません。
【二重根号になった数のもつれをほどくだけ】
任意のaとbの場合を考えると、
a2-4bの平方根の平方根記号(根号)が外れる場合はまれな場合であって、
ほとんどの場合は、その根号が外せないので、二重根号を外す事ができません。
それでは、この方法は何の役に立つのだろうか?
という疑問がわくと思います。
その疑問に対する答えは、以下のようなものです。
「計算のもつれによって、二重根号でない数が二重根号になる場合があります。
そのように「もつれた」数の「もつれ」をほどくだけです。」
【簡易な計算方法】
公式をすぐ導き出せるようにして公式を覚えないで良い方法を以下で示します。
a=x+y, (5)
とした式(5)の未知数xとyを、以下の式のように未知数 z だけであらわす。すなわち、2つあった未知数をzの1つだけにします。
x=(a+z)/2,
y=(a-z)/2,
これを、
 (7)’
(7)’
のxとyに代入してzで表せば、
 (9)
(9)
になります。
この式9が、1つの未知数zだけで二重根号を外す式をあらわしています。
(この式9を覚えれば、公式は覚えないで良いと思います。)
式9の両辺を2乗して未知数zを求めます。
これで得られたzを式9に代入すれば、以下の公式が得られます。

または、
《簡易公式2》

です。根号の中の式に、根号の中にuがある項を持つので2重根号になっていた式は、根号の中の式に、根号の中にa2-uがある項を持つ式に変換できます。
二重根号を外す計算は、この公式を使って式を書き変えているだけです。
そして、
a2-4b(または、a2-u)の平方根の根号が外せる場合に限って、二重根号が外れます。
なお、平方根の根号が外せる場合には、以下の場合の様に、無理数の2乗の数(自然数の2乗である平方数とは異なるが)になって平方根の根号が外れる場合もあります。

(蛇足)この公式により、上の式の右辺の、対になっている2つの二重根号の式は、上の式の左辺の1つの二重根号の式にまとめることができます。
例えば、下の式では、下の式の左辺の2項を右辺の1つの項にまとめることができます。

ただし、この式の左辺を2乗すれば、すぐに右辺の式のルートの中が得られますので、この公式を覚えて使う必要はありません。
【二重根号の外し方(方法3)】
4次方程式方の解き方が、二重根号付きの式を経て解に至る解き方と、二重根号を経ずに解が得られる解き方との、2つの解き方があることを利用して解きます。
この方法は、4次方程式を解く計算でもつれさせてしまった答えの数を、もとの4次方程式に戻してから、答えをもつれさせない手順で4次方程式を解く方法です。

【簡易な計算方法】
この計算方法から、計算の本質部分を抽出した結果、
以下の様な計算方法が見つかりました。
(1)
(2)
(3)
(解答おわり)
【二重根号の外し方(方法4)】
方法4は、方法3に近い方法です。
以下の様にして二重根号を外します。
この式の中のx2の値は式2で分かっているので、その値をこの式に代入します。
上の計算の途中で得た式3の右辺のx2の係数の平方根は二重根号にはなりませんでした。
ほかの式の場合も、同様に計算して式3に相当する式のx2の係数の平方根が二重根号にならなければ、二重根号が外せます。
(解答おわり)
二重根号が外れない問題
リンク:二重根号の外し方
リンク:高校数学の目次
〔ページ内リンク〕
▷二重根号の外し方(方法1)
▷二重根号の外し方(方法2)
▷二重根号が外せない場合
▷簡易な計算方法
▷簡易公式2
▷二重根号の外し方(方法3)
▷二重根号の外し方(方法4)
【問】 以下の式の二重根号を外せ。
【注意】二重根号が外せない場合については後に説明しますので、先ずは、以下の、二重根号を外せる場合の説明を読んで下さい。
【二重根号の外し方(方法1)】
先ず、
と変形し、その右側の項の形にします。右側の項を、
(以下の計算方針では、√3という数を含んでいない数(x)と(a)を使って表わせる場合の解だけを求める計算をします。
√3を(x)か(a)が含まざるを得なかったら、そこで計算を終わりにする覚悟をして、以下の計算をします)
この式の両辺を二乗します。
(x)と(a)とが√3を含んでいない数であらわされるならば、
4=a・(1+3x) (1)と、
がなりたつと考えることができます。
2つ目の式を更に簡単にすると、

1=a2x (2)
になります。
(2)より、
(3)を(1)に代入します。
この式から、
この式4を因数分解して解くと:
(a-1)(a-3)=0
a=1 or 3
a=1の場合を(3)に代入すると、
x=1
よって、
です。
(a=3の場合も:x=1/9になって、それを代入すると同じ答えになります)
そのため、
になりました。
【二重根号の外し方(方法2)】
二重根号を外すもう1つの方法を説明します。
(原理について)
という形をしている2重根号は、以下の条件が成り立つ場合に外すことができます。
a=x+y (5)
b=x・y (6)
となるxとyを探します。
そのxとyがあれば、
 (7)
(7)です。

となるからです。
式5と6の解のx、yを求めるということは、
x2-a・x+b=0 (8)
の解x、yを求めることと同じです。この式8は、式4と同じ式になります。
(具体例について)
具体的な今回の以下の問題の場合は、以下のようにして解きます。
の場合は、
と変形します。
この様に、ルートの中の式は、ルートの2倍の項を含む式に変形して、答えを求めます。
を解く場合は、
(x2-4・x+3=0 (式4)を解くのと同じですが)
x+y= a=4=3+1
xy= b=3=3・1
がなりたちますので
x=3
y=1
が見つかりました。
です。
そのため、
です。
【二重根号が外せない場合】
という形をしている2重根号は、
|a2-4b|の平方根の式が、その平方根記号を外せる場合に2重根号を外すことができます。
(1) 先ず、
a2-4b≧0の場合で、その平方根の式が、その平方根記号を外せる場合に平方根を外すことができます。
a2-4b=(x+y)2-4xy=(x-y)2
だからです。
すなわち、
(a2-4b)の平方根=|x-y|
であり、一方、
a=x+y
だったので、この2つの式からxとyが求められるからです。
(2) 次に、√(a(√b)+2b)を考えることで、結局、
4b-a2≧0の場合で、その平方根の式が、その平方根記号を外せる場合も、2重根号を外すことができます。
しかし、|a2-4b|の平方根の式から平方根記号が外せ無いときは、先の式の二重根号を外すことができません。
【二重根号になった数のもつれをほどくだけ】
任意のaとbの場合を考えると、
a2-4bの平方根の平方根記号(根号)が外れる場合はまれな場合であって、
ほとんどの場合は、その根号が外せないので、二重根号を外す事ができません。
それでは、この方法は何の役に立つのだろうか?
という疑問がわくと思います。
その疑問に対する答えは、以下のようなものです。
「計算のもつれによって、二重根号でない数が二重根号になる場合があります。
そのように「もつれた」数の「もつれ」をほどくだけです。」
【簡易な計算方法】
公式をすぐ導き出せるようにして公式を覚えないで良い方法を以下で示します。
a=x+y, (5)
とした式(5)の未知数xとyを、以下の式のように未知数 z だけであらわす。すなわち、2つあった未知数をzの1つだけにします。
x=(a+z)/2,
y=(a-z)/2,
これを、
 (7)’
(7)’のxとyに代入してzで表せば、
 (9)
(9)になります。
この式9が、1つの未知数zだけで二重根号を外す式をあらわしています。
(この式9を覚えれば、公式は覚えないで良いと思います。)
式9の両辺を2乗して未知数zを求めます。
これで得られたzを式9に代入すれば、以下の公式が得られます。

または、
《簡易公式2》

です。根号の中の式に、根号の中にuがある項を持つので2重根号になっていた式は、根号の中の式に、根号の中にa2-uがある項を持つ式に変換できます。
二重根号を外す計算は、この公式を使って式を書き変えているだけです。
そして、
a2-4b(または、a2-u)の平方根の根号が外せる場合に限って、二重根号が外れます。
なお、平方根の根号が外せる場合には、以下の場合の様に、無理数の2乗の数(自然数の2乗である平方数とは異なるが)になって平方根の根号が外れる場合もあります。

(蛇足)この公式により、上の式の右辺の、対になっている2つの二重根号の式は、上の式の左辺の1つの二重根号の式にまとめることができます。
例えば、下の式では、下の式の左辺の2項を右辺の1つの項にまとめることができます。

ただし、この式の左辺を2乗すれば、すぐに右辺の式のルートの中が得られますので、この公式を覚えて使う必要はありません。
【二重根号の外し方(方法3)】
4次方程式方の解き方が、二重根号付きの式を経て解に至る解き方と、二重根号を経ずに解が得られる解き方との、2つの解き方があることを利用して解きます。
この方法は、4次方程式を解く計算でもつれさせてしまった答えの数を、もとの4次方程式に戻してから、答えをもつれさせない手順で4次方程式を解く方法です。

【簡易な計算方法】
この計算方法から、計算の本質部分を抽出した結果、
以下の様な計算方法が見つかりました。
(1)
(2)
(3)
(解答おわり)
【二重根号の外し方(方法4)】
方法4は、方法3に近い方法です。
以下の様にして二重根号を外します。
この式の中のx2の値は式2で分かっているので、その値をこの式に代入します。
上の計算の途中で得た式3の右辺のx2の係数の平方根は二重根号にはなりませんでした。
ほかの式の場合も、同様に計算して式3に相当する式のx2の係数の平方根が二重根号にならなければ、二重根号が外せます。
(解答おわり)
二重根号が外れない問題
リンク:二重根号の外し方
リンク:高校数学の目次









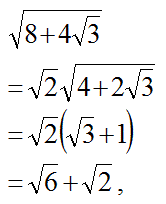







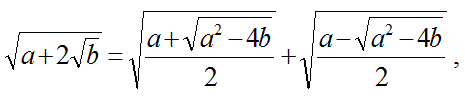

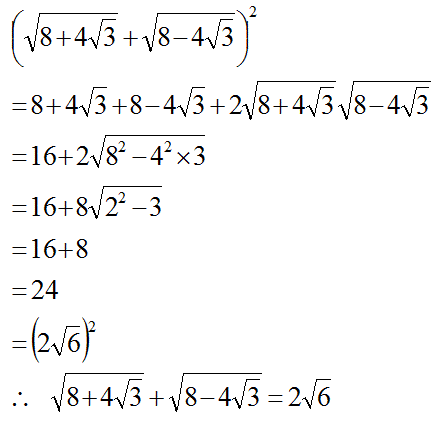





0 件のコメント:
コメントを投稿