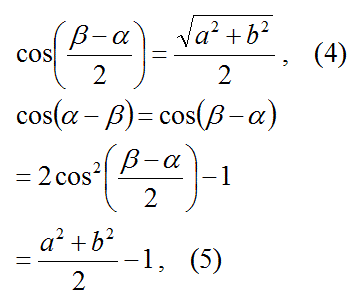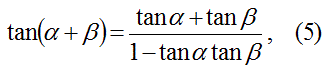（以下は、ここをクリックした先のページの問題の解答です）
【問１】三角形ＡＢＣにおいて、次の式が成り立つことを証明せよ。
（注意）ｃｏｔＡは
で定義されています。
【重要な注意】
三角関数の計算の自由度は低く、加法定理などで変換できる式は少ないです。
（この問題が加法定理で解ける問題であるかを調べる）
先ず、この問題は加法定理で解ける問題であるかを簡単に確認します。
ｃｏｔＡｃｏｔＢ＝１／（ｔａｎＡｔａｎＢ） の式のｔａｎＡｔａｎＢの積の式がｔａｎの加法定理で使われていたことを思い出す。
この（式２）がこの問題の解答に使えないかどうかを、以下のように検討する。
三角形ＡＢＣであるので、Ａ＋Ｂ＝π－Ｃを式２に代入して左辺をＣであらわす。
左辺＝ｔａｎ（π－Ｃ）＝ｔａｎ（－Ｃ）＝－ｔａｎＣ
この式を式２に代入する。
分母を両辺に掛け算して分母を分子に移す。
右辺に１／（ｔａｎＡｔａｎＢ）があらわれるようにするために、式全体をｔａｎＣｔａｎＡｔａｎＢで割り算する。
これは式１である。加法定理が使えないかどうかを検討しているうちに、求める（式１）が得られてしまった。
加法定理で解ける問題というものは、問題が加法定理で解けるかどうかを検討中に解けてしまう問題が多い。
リンク：
高校数学の目次
以下は、ここをクリックした先のページの問題の解答です。
【問題１】
以下の式１と式２が成り立っているとき、ｇ ≡ ｃｏｓ（α＋β）を定数ａとｂであらわせ。
【解答１】
先ず、以下の式４を計算する。
次に、以下の式５を計算する。
この式５からｃｏｓ（α＋β）をあらわす以下の式を導き、その式に式４を代入する。
（解答おわり）
【解答２】
解答１の解き方は、偶然に解答できたような解答でした。
そのため、以下で、必然的に解を得る解答をしてみます。
（解答はじめ）
式１を変形する。
式２を変形する。
式７と式８から、以下の式９を得る。
求める式 ｇ を変形する。
（解答おわり）
【解答３】
解答１と解答２は、計算力に頼った解答であった。以下の解答３は、この問題の本質をもっと良く見通して解答する解答を示す。
（解答はじめ）
この問題の条件を以下の図であらわす。
以下の計算により、問題の解が得られる。
（解答おわり）
（補足）
三角関数の計算問題でも、図形にあらわせる限り、問題を図形であらわして解くのが良いと考えます。
リンク：
高校数学の目次
以下は、ここをクリックした先のページの問題の解答です。
【問題１】
以下の式１と式２が成り立っているとき、ｆ ≡ ｃｏｓ（α－β）を定数ａとｂであらわせ。
【解答１】
（解答おわり）
【解答２】
解答１は、計算力に頼った解答であった。以下の解答２は、この問題の本質をもっと良く見通して解答する解答を示す。
（解答はじめ）
この問題の条件を以下の図であらわす。
以下の計算により、問題の解が得られる。
（解答おわり）
（補足）
三角関数の計算問題でも、図形にあらわせる限り、問題を図形であらわして解くのが良いと考えます。
リンク：
高校数学の目次
これは、ここをクリックした先の問題の解答です。
【問１】ｘ２－（√３）ｘ－２＝０の２つの解を、ｔａｎα，ｔａｎβとするとき、
の値を求めよ。
【解答１】
（求める答えを、より易しい答えにできないかを考える）
問題を解くときには、いつも、この発想から始めること。
この段階では、どう解答するかの見通しを立てます。
ｔａｎα，ｔａｎβが
方程式 ｘ２－（√３）ｘ－２＝０ （式２）
の２つの解であるとき、
－（ｘの係数）： √３＝ｔａｎα＋ｔａｎβ （式３）
定数項： －２＝ｔａｎαｔａｎβ （式４）
となる関係を思い出して使う。
つぎに、ｔａｎの加法定理を思い出す。
（ｔａｎα＋ｔａｎβ）と、ｔａｎαｔａｎβが求められれば、ｔａｎ（α＋β）が求められることを見通す。
こうしてｔａｎ（α＋β）が求められるというめどが立ったので、ｔａｎ（α＋β）を求めて、それから、（α＋β）を求めて、ｓｉｎ（α＋β）もｃｏｓ（α＋β）も求めて、それらの値を式１に代入して答えを得る
という、解答の見通しを立てます。
（ｔａｎ（α＋β）を計算する）
式３と式４を式５に代入する。
∴ （α＋β）＝π／６ または ７π／６
（１）（α＋β）＝π／６のとき
ｓｉｎ（α＋β）＝１／２ （式６）
ｃｏｓ（α＋β）＝√３／２ （式７）
方程式６と７を式１に代入
（式１）
（２）（α＋β）＝７π／６のときｓｉｎ（α＋β）＝－１／２ （式８）
ｃｏｓ（α＋β）＝－√３／２ （式９）
方程式８と９を式１に代入
（式１）
（解答おわり）
【解答２】
ｔａｎの値を使って解く問題の式は、以下の式２のように、ｃｏｓの２乗の式とｔａｎの式に変形して計算する。
ここで、ｔａｎ（α＋β）の式は以下の式３であらわされる。
ｘ２－（√３）ｘ－２＝０の２つの解を、ｔａｎα，ｔａｎβとするので、以下の式４が成り立つ。
この式５と６を式３に代入する。
この式７を式２に代入する。
（解答おわり）
リンク：
高校数学の目次
（注意）ｃｏｔＡは
この（式２）がこの問題の解答に使えないかどうかを、以下のように検討する。
分母を両辺に掛け算して分母を分子に移す。
これは式１である。加法定理が使えないかどうかを検討しているうちに、求める（式１）が得られてしまった。
