これは、ここをクリックした先の問題の解答です。
【問1】x2-(√3)x-2=0の2つの解を、tanα,tanβとするとき、

の値を求めよ。
【解答1】
(求める答えを、より易しい答えにできないかを考える)
問題を解くときには、いつも、この発想から始めること。
この段階では、どう解答するかの見通しを立てます。
tanα,tanβが
方程式 x2-(√3)x-2=0 (式2)
の2つの解であるとき、
-(xの係数): √3=tanα+tanβ (式3)
定数項: -2=tanαtanβ (式4)
となる関係を思い出して使う。
つぎに、tanの加法定理を思い出す。
(tanα+tanβ)と、tanαtanβが求められれば、tan(α+β)が求められることを見通す。
こうしてtan(α+β)が求められるというめどが立ったので、tan(α+β)を求めて、それから、(α+β)を求めて、sin(α+β)もcos(α+β)も求めて、それらの値を式1に代入して答えを得る
という、解答の見通しを立てます。
(tan(α+β)を計算する)
式3と式4を式5に代入する。
∴ (α+β)=π/6 または 7π/6
(1)(α+β)=π/6のとき
sin(α+β)=1/2 (式6)
cos(α+β)=√3/2 (式7)
方程式6と7を式1に代入
(式1)
(2)(α+β)=7π/6のときsin(α+β)=-1/2 (式8)
cos(α+β)=-√3/2 (式9)
方程式8と9を式1に代入
(式1)
(解答おわり)
【解答2】
tanの値を使って解く問題の式は、以下の式2のように、cosの2乗の式とtanの式に変形して計算する。
ここで、tan(α+β)の式は以下の式3であらわされる。
x2-(√3)x-2=0の2つの解を、tanα,tanβとするので、以下の式4が成り立つ。
この式5と6を式3に代入する。
この式7を式2に代入する。
(解答おわり)
リンク:
高校数学の目次
【問1】x2-(√3)x-2=0の2つの解を、tanα,tanβとするとき、

の値を求めよ。
【解答1】
(求める答えを、より易しい答えにできないかを考える)
問題を解くときには、いつも、この発想から始めること。
この段階では、どう解答するかの見通しを立てます。
tanα,tanβが
方程式 x2-(√3)x-2=0 (式2)
の2つの解であるとき、
-(xの係数): √3=tanα+tanβ (式3)
定数項: -2=tanαtanβ (式4)
となる関係を思い出して使う。
つぎに、tanの加法定理を思い出す。
(tanα+tanβ)と、tanαtanβが求められれば、tan(α+β)が求められることを見通す。
こうしてtan(α+β)が求められるというめどが立ったので、tan(α+β)を求めて、それから、(α+β)を求めて、sin(α+β)もcos(α+β)も求めて、それらの値を式1に代入して答えを得る
という、解答の見通しを立てます。
(tan(α+β)を計算する)
式3と式4を式5に代入する。
∴ (α+β)=π/6 または 7π/6
(1)(α+β)=π/6のとき
sin(α+β)=1/2 (式6)
cos(α+β)=√3/2 (式7)
方程式6と7を式1に代入
(式1)
(2)(α+β)=7π/6のときsin(α+β)=-1/2 (式8)
cos(α+β)=-√3/2 (式9)
方程式8と9を式1に代入
(式1)
(解答おわり)
【解答2】
tanの値を使って解く問題の式は、以下の式2のように、cosの2乗の式とtanの式に変形して計算する。
ここで、tan(α+β)の式は以下の式3であらわされる。
x2-(√3)x-2=0の2つの解を、tanα,tanβとするので、以下の式4が成り立つ。
この式5と6を式3に代入する。
この式7を式2に代入する。
(解答おわり)
リンク:
高校数学の目次
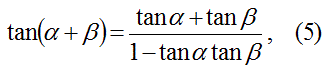








0 件のコメント:
コメントを投稿