これは、ここをクリックした先のページの問題の解答です。
【問１】
上の三角形において、図の角度の条件が成り立つＤ点の位置座標を求めよ。
ただし、点Ａ，Ｂ，Ｃの位置座標を、Ａ（０，０）と、Ｂ （１，０）と、Ｃ（０，√３）とする。
（解答方針）
ベストな解答方針は、余弦定理で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
この方針は、高校２年になってベクトル方程式を学んだ後でも変わりません。問題解答のベストな方針は、ベクトル方程式で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
更に言うと、大学入試の段階に至って、ピタゴラスの定理を駆使して解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
正弦定理（又は円周角の定理）は、それだけ優れた画期的手法だからです。
また、この問題の様に、
①三角形の頂点の角度θと
②その頂点に対向する辺の長さａが与えられている場合は、
直ぐに、正弦定理を使って、
③その三角形に外接する円の半径Ｒが、
Ｒ＝ａ／（２ｓｉｎθ）
で求められ、
④その円の中心位置も直ぐに求められる
という事を連想するように発想して下さい。
すなわち、頂角θと対向辺ａが分かっている三角形毎に下図の外接円を想像するようにして下さい。
そして、この図を想像したら、次は、この図の円の中心座標を求めようと考えるように、心を整えておいて下さい。
【第１の解答の試み】
上に書いたベストな解答方針が優れていることを示すために、あえて、このベストな解答方針に逆らって、正弦定理を考えずに、先ず余弦定理で解くことを考えてみます。
先ず、一番ダメな解答の試みを書きます。この試みは途中で解答を断念する道草を食う例ですので、解答にもならないことに付き合いたくない人は、この第１の解答の試みの説明をスキップして次の解答から読み始めてください。
（余弦定理を使って問題の条件を記述する方程式を書く）
先ず、以下の座標軸を考える。
この図の三角形ＤＢＣについて１２０°の角ＢＤＣに関する余弦定理の方程式を作成する。
この式を展開する。
これで、ようやく、余弦定理に角ＢＤＣが１２０°である条件を入れた方程式が作れた。
しかし、この方程式はどうしようもなく複雑で、とても使いこなせそうにありません。
そのため、これ以上の、この方針による解答の試みは断念することにします。
（解答を断念）
【第２の解答】
次も、未だ、ベストな解答方針の正弦定理を使うことに逆らいます。
第２の解答では、ピタゴラスの定理を駆使して問題を解くために、問題の形を変えて、解き易くする工夫をします。
この図形を回転させて、また、相似な図形にして、下図のように線分ＡＤを水平方向に向けた図形で考えます。
この図形は、元の図形に相似な図形であり、ＡＤの長さを１にした図形です。
以下で、この図の三角形ＯＢＣの角Ｏが直角になる条件の方程式１と、三角形ＯＢＣが元の図形ＡＢＣに相似になる辺の条件の方程式２を作って、方程式を解きます。
先ず式１を変形します。
次に、式２を変形します。
式３を以下の式３’に変形して、それを式４に代入して解きます。
次に、この方程式を解きますが、
方程式の１つの解が得られるだけで良く、
簡単な解を推測によって見つけます。
既に、上の式でも、ｓ１＝１を上の式に代入して式が成り立つので、これが解であることがわかります。
この解を以下のように図に書き込みます。
更に座標にかかわる詳しい寸法を計算します。
こうして得られたＤ点の座標を、相似変換することで、元の問題の図形のＤ点の座標を計算します。
（第２の解答おわり）
以上で、苦労して何とか答えを得ることができましたが、この計算はベストな解答方針ではありませんでした。
以下では、ベストな解答方針である、「先ず、正弦定理（又は円周角の定理）を使って問題が解けないかを考える」に従って問題を解きます。
【ベストな解答（第３の解答）】
三角形ＤＢＣの角Ｄが１２０°であることを正弦定理であらわした式を考えます。そうすると、三角形の外接円の半径が上式で求められます。
円周角の定理を使ってこの外接円を詳しく調べます。
下図のように、外接円に内接する正三角形ＥＣＢを考えます。
円周角の定理を使うと、角ＢＤＥと角ＢＣＥは６０°で等しく、角ＣＤＥと角ＣＢＥは６０°で等しい。
また、外接円の中心Ｍの位置は上図で示す位置にあることが分かります。
この図から、Ｄ点の位置座標を計算する方程式を作って計算します。
この方程式の解は、以下のようになります。
（解答おわり）
以上のように、正弦定理（又は円周角の定理）を使うと問題が簡単に解けました。
このことから、
ベストな解答方針は、余弦定理で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みることであることが分かります。
【拡張円周角の定理を思い出す】
拡張円周角の定理によって、三角形の各角度が外接円の点のまわりの角度に反映されることを思い出しましょう。
それを思い出して、点Ｄを円周角上の点であるとして、以下の図のように、点Ｄを円周上に持つ円Ｍと、その円に内接する三角形ＣＢＥを発想します。
この図の関係から、中心Ｍからの半径Ｒの円Ｍと、直線ＡＥの交点Ｄを計算する方程式を立てることで点Ｄの座標を計算することができることが分かります。
その方程式は、上の回答の様に計算します。
この解答方針は、高校２年で学ぶベクトル方程式に対しても、同様に通用します。高校２年のベクトル方程式で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
なお、この問題は、余弦定理等を使って解くことは困難ですが、複素数平面を使うと解けます。
複素数平面を使う解き方は、ここをクリックした先のページにあります。
【ベクトルの回転変換の公式を使った解答（第４の解答）】
第４の解答は、正弦定理や円周角の定理で解ける問題はベクトル計算で解くのが難しいというベクトル計算の欠点を、各ベクトルに、それを９０°回転させたベクトルを組み合わせることで補って、ベクトル計算でも問題を解けるようにします。
先ず、Ｄ点を位置ベクトルＺであらわします。また、ベクトルＺを左回りに９０度回転したベクトルＺＶを使います。
ベクトルの回転変換の公式を使って、未知数ｓとｔを使った以下の方程式１１と式１２を作ります。
（この方程式１１と１２には円周角の定理の持つ本質的な情報が含まれています）
式１１と１２を式１５と式１６に変形した。
以下のようにベクトルＺＶを消去してベクトルＺを求めます。
この式１７と式１８を式１６に代入して、ベクトル方程式１９を作り、未知数ｓとｔを求める。
式２０と２１を更に変形する。
ｔ＝０の場合は不適。
ｔ≠０の場合を計算する。
以上で得たｓとｔを式１７に代入して位置ベクトルＺの座標を計算する。
（解答おわり）
【第５の解答】
第５の解答は、正弦定理や円周角の定理で解ける問題はベクトル計算で解くのが難しいというベクトル計算の欠点を、円周角の定理をあらわす式（正弦定理で使う外接円）を、ベクトル計算の外から導入することで補って、ベクトルの問題を解けるようにします。
円周角の定理から、上図の様に、点Ｋを中心にした円が点Ｄを通り、点Ｇを中心にした円が点Ｄを通ります。
この円周角の定理（正弦定理）の結論から、ベクトルＡＤの座標（ｘ，ｙ）が満足する方程式を書きます。
式３と式４の方程式が作れました。
この方程式を以下の様に計算して解きます。
この２つの解のうち、ｘ＝０は不適です。
残りの解により、解を計算します。
（解答おわり）
（補足）
第５の解答では、円周角の定理（正弦定理の外接円）に基づいた方程式１と２（それを表した式３と４）を導入して問題を解いたので、ベストな解答である第３の解答と同じく問題を易しく解ける同質な解答ができました。
第５の解答で作った方程式１と２は、円周角の定理（正弦定理）に基づいて作成した方程式であって、第１の解答の試みにおいて作った余弦定理の方程式とは根本的に異なります。
余弦定理によっては直接には円周角の定理をあらわすことはできません。第１の解答の試みでは円周角の定理（正弦定理の外接円）をあらわす方程式を作れなかったので、解答がとても難しくなりました。
リンク：
高校数学の目次
【問１】
ただし、点Ａ，Ｂ，Ｃの位置座標を、Ａ（０，０）と、Ｂ （１，０）と、Ｃ（０，√３）とする。
（解答方針）
ベストな解答方針は、余弦定理で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
この方針は、高校２年になってベクトル方程式を学んだ後でも変わりません。問題解答のベストな方針は、ベクトル方程式で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
更に言うと、大学入試の段階に至って、ピタゴラスの定理を駆使して解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
正弦定理（又は円周角の定理）は、それだけ優れた画期的手法だからです。
また、この問題の様に、
①三角形の頂点の角度θと
②その頂点に対向する辺の長さａが与えられている場合は、
直ぐに、正弦定理を使って、
③その三角形に外接する円の半径Ｒが、
Ｒ＝ａ／（２ｓｉｎθ）
で求められ、
④その円の中心位置も直ぐに求められる
という事を連想するように発想して下さい。
すなわち、頂角θと対向辺ａが分かっている三角形毎に下図の外接円を想像するようにして下さい。
【第１の解答の試み】
上に書いたベストな解答方針が優れていることを示すために、あえて、このベストな解答方針に逆らって、正弦定理を考えずに、先ず余弦定理で解くことを考えてみます。
先ず、一番ダメな解答の試みを書きます。この試みは途中で解答を断念する道草を食う例ですので、解答にもならないことに付き合いたくない人は、この第１の解答の試みの説明をスキップして次の解答から読み始めてください。
（余弦定理を使って問題の条件を記述する方程式を書く）
先ず、以下の座標軸を考える。
しかし、この方程式はどうしようもなく複雑で、とても使いこなせそうにありません。
そのため、これ以上の、この方針による解答の試みは断念することにします。
（解答を断念）
【第２の解答】
次も、未だ、ベストな解答方針の正弦定理を使うことに逆らいます。
第２の解答では、ピタゴラスの定理を駆使して問題を解くために、問題の形を変えて、解き易くする工夫をします。
以下で、この図の三角形ＯＢＣの角Ｏが直角になる条件の方程式１と、三角形ＯＢＣが元の図形ＡＢＣに相似になる辺の条件の方程式２を作って、方程式を解きます。
方程式の１つの解が得られるだけで良く、
簡単な解を推測によって見つけます。
既に、上の式でも、ｓ１＝１を上の式に代入して式が成り立つので、これが解であることがわかります。
以上で、苦労して何とか答えを得ることができましたが、この計算はベストな解答方針ではありませんでした。
以下では、ベストな解答方針である、「先ず、正弦定理（又は円周角の定理）を使って問題が解けないかを考える」に従って問題を解きます。
【ベストな解答（第３の解答）】
円周角の定理を使ってこの外接円を詳しく調べます。
下図のように、外接円に内接する正三角形ＥＣＢを考えます。
また、外接円の中心Ｍの位置は上図で示す位置にあることが分かります。
この図から、Ｄ点の位置座標を計算する方程式を作って計算します。
以上のように、正弦定理（又は円周角の定理）を使うと問題が簡単に解けました。
このことから、
ベストな解答方針は、余弦定理で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みることであることが分かります。
【拡張円周角の定理を思い出す】
拡張円周角の定理によって、三角形の各角度が外接円の点のまわりの角度に反映されることを思い出しましょう。
それを思い出して、点Ｄを円周角上の点であるとして、以下の図のように、点Ｄを円周上に持つ円Ｍと、その円に内接する三角形ＣＢＥを発想します。
その方程式は、上の回答の様に計算します。
この解答方針は、高校２年で学ぶベクトル方程式に対しても、同様に通用します。高校２年のベクトル方程式で解けそうな問題があっても、先ずは正弦定理（又は円周角の定理）を使って問題を解くよう試みてください。
なお、この問題は、余弦定理等を使って解くことは困難ですが、複素数平面を使うと解けます。
複素数平面を使う解き方は、ここをクリックした先のページにあります。
【ベクトルの回転変換の公式を使った解答（第４の解答）】
第４の解答は、正弦定理や円周角の定理で解ける問題はベクトル計算で解くのが難しいというベクトル計算の欠点を、各ベクトルに、それを９０°回転させたベクトルを組み合わせることで補って、ベクトル計算でも問題を解けるようにします。
ベクトルの回転変換の公式を使って、未知数ｓとｔを使った以下の方程式１１と式１２を作ります。
（この方程式１１と１２には円周角の定理の持つ本質的な情報が含まれています）
以下のようにベクトルＺＶを消去してベクトルＺを求めます。
ｔ＝０の場合は不適。
ｔ≠０の場合を計算する。
【第５の解答】
第５の解答は、正弦定理や円周角の定理で解ける問題はベクトル計算で解くのが難しいというベクトル計算の欠点を、円周角の定理をあらわす式（正弦定理で使う外接円）を、ベクトル計算の外から導入することで補って、ベクトルの問題を解けるようにします。
この円周角の定理（正弦定理）の結論から、ベクトルＡＤの座標（ｘ，ｙ）が満足する方程式を書きます。
この方程式を以下の様に計算して解きます。
残りの解により、解を計算します。
（補足）
第５の解答では、円周角の定理（正弦定理の外接円）に基づいた方程式１と２（それを表した式３と４）を導入して問題を解いたので、ベストな解答である第３の解答と同じく問題を易しく解ける同質な解答ができました。
第５の解答で作った方程式１と２は、円周角の定理（正弦定理）に基づいて作成した方程式であって、第１の解答の試みにおいて作った余弦定理の方程式とは根本的に異なります。
余弦定理によっては直接には円周角の定理をあらわすことはできません。第１の解答の試みでは円周角の定理（正弦定理の外接円）をあらわす方程式を作れなかったので、解答がとても難しくなりました。
リンク：
高校数学の目次
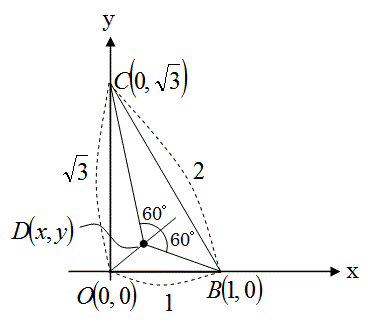
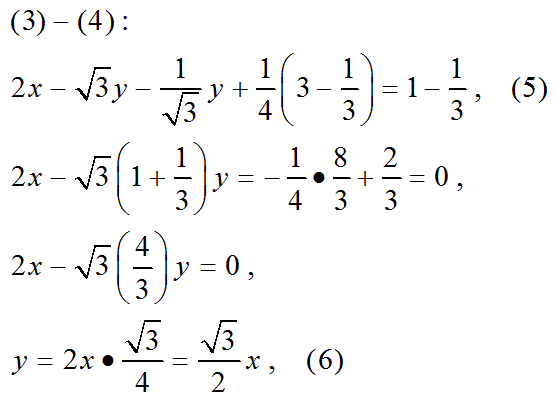
0 件のコメント:
コメントを投稿