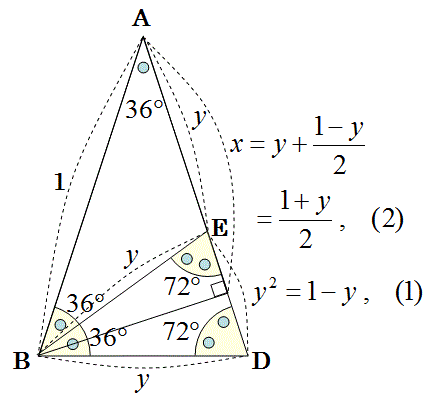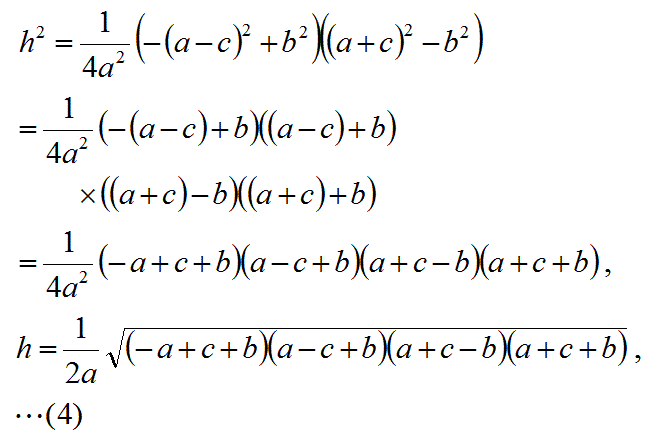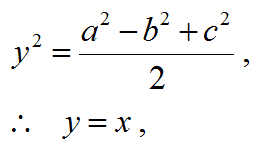以下は、ここをクリックした先の問題の解答です。
【問１】（難問）
上の図のような、角Ｃ直角で頂角Ａが３６°の直角三角形ＡＢＣの斜辺ＡＢの長さが１の場合に、辺ＡＣの長さを求めなさい。
《解答手順》
図形問題では、先ず、足りない図形の補助線を埋め込み、同じ角度には同じ印を付け、なるべく対称な形に、図形を完成させる。その次に問題の解き方を考えるように心がけてください。
【解答】
まず、以下の様に、３６°の頂角Ａを頂角にする二等辺三角形ＡＢＤを考えます。
上図のように、二等辺三角形ＢＤＥを考えると、その頂角∠ＤＢＥ＝３６°になります。
そのため、
△ＡＢＤ∽△ＢＤＥ
です。
また、∠ＡＢＥ＝３６°＝∠ＢＡＥ
ですので、
△ＥＡＢは二等辺三角形になり、
ＡＥ＝ＥＢ
です。
また、
ＥＢ＝ＤＢ＝ｙ
です。
そのため、以下の図の式１と式２が得られます。
式２のように、ｙからｘが計算できます。
そのため、ｙの式１を解けば良いことがわかります。
（解答おわり）
リンク：
中学数学の目次
以下は、ここをクリックした先の問題の解答です。
【問１】（難問）
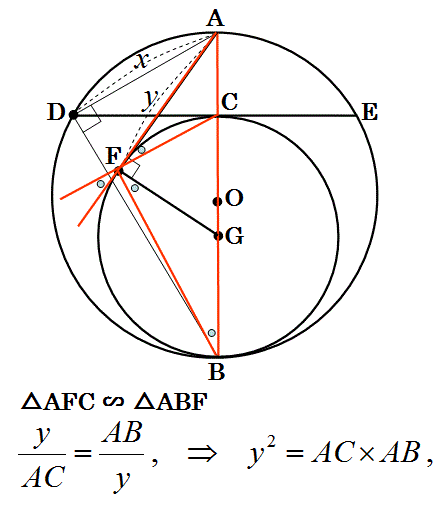
上の図のような、円に内接する四角形ＡＢＣＤにおいて、
ＡＢ＝ＢＣ＝３、
ＣＤ＝５、
ＤＡ＝８
のとき，∠ A の大きさを求めなさい。
《解答手順》
図形問題では、先ず、足りない図形の補助線を埋め込み、同じ角度には同じ印を付け、なるべく対称な形に、図形を完成させる。その次に問題の解き方を考えるように心がけてください。
【解答】
まず、以下の様に、同じ角度に印を付けます。
そして、同じ角度の図形を重ねて、図形をほぼ対称な形に完成させてから解きます。
ここまで書いたら、三角形ＡＢＥが正三角形になっています。
そのため、
∠Ａ＝６０°
です。
（解答おわり）
リンク：
中学数学の目次
以下は、ここをクリックした先の問題の解答です。
【問１】
上図の三角形ＡＢＣの高さｈを辺の長さａ，ｂ，ｃを使ってあらわす式を求めよ。
【解答】
以下の計算によって、先ず、ａ１を計算する。
次に、以下のようにｈの二乗を計算する。
この式３を高さの公式としておぼえておくと便利です。
ただし、ｈの式３は、以下の様に３通りにあらわすことができます。
すなわち、三角形ABCの面積Sが、
Ｓ＝ａｈ／２
であり、そのＳのあらわし方が以下の通り３つあると考えられます。
面積Ｓの３つのあらわしかたの１つの式３ｃを使って、
ｈを式３’ｃであらわすことができます。
（以下では、式２から別の分岐に進む計算をします）
式２は以下の因数分解ができ、以下の高さの公式４が得られます。
（解答おわり）
リンク：
中学数学の目次
以下は、ここをクリックした先の問題の解答です。
【問１】（これも難問だと思う）
上図の三角形ＡＢＣがある場合に、その三角形ＡＢＣを底面とする四面体で、下図のように、直方体の角Ｈの断片の四面体ＨＡＢＣを作る展開図の直角三角形の頂点Ｈ，Ｈ’，Ｈ’’を作図せよ。
【解答】
（１）図のように、辺ＢＣを中心にして三角形ＢＨＣを回転させて真上（ＡＢＣの面に垂直な方向）から見ると、点ＨはＢＣに垂直な直線上を動くように見える。
ここで、三角形ＢＨＣは、頂角Ｈを直角とする直角三角形なので、辺ＢＣを軸にして回転させると、下図のように辺ＢＣを直径とし点Ｌを中心とする円Ｌ上の点Ｈを頂角とする直角三角形ＢＣＨに重なる。
（２）同様にして、辺ＡＢを中心軸にして直角三角形ＡＢＨを回転させて平面ＡＢＣ上に展開すると下図のように、辺ＡＢを直径とし点Ｎを中心とする円Ｎ上の点Ｈ’’を頂角とする直角三角形ＡＢＨ’’に重なる。
この図で、
円Ｌの半径＝ＬＨ＝ＬＢであり、
円Ｎの半径＝ＮＨ’’＝ＮＢであるので、
三角形ＮＬＨは三角形ＮＬＢと３辺の長さが同じで合同である。
三角形ＮＬＨを直線ＮＬを中心軸にして回転させると、下図のように点Ｈが回転して点Ｂに重なる。
面ＡＢＣの真上から見ると、三角形ＮＬＨを直線ＮＬを中心軸にして回転させる場合に点Ｈが、直線ＮＬに垂直で点Ｂを通る直線上を動くように見える。
直線ＮＬは三角形ＡＢＣの中線なので、辺ＡＣに平行である。
それゆえ、点Ｈは辺ＡＣに垂直で点Ｂを通る直線上を動くように見える。
（３）同様にして、点Ｈを別の直線を軸にして回転させて真上から見ると、以下の展開図のようになる。
三角形ＮＭＨを、直線ＮＭを中心軸にして回転させると、点Ｈは回転して点Ａに重なる。
真上から見ると、点Ｈは辺ＢＣに平行な直線ＮＭに垂直で点Ａを通る直線ＡＨ上を動くように見える。
（４）三角形ＭＬＨを、直線ＭＬを中心軸にして回転させると、点Ｈは回転して点Ｃに重なる。
真上から見ると、点Ｈは辺ＡＢに平行な直線ＭＬに垂直で点Ｃを通る直線ＣＨ’’上を動くように見える。
（５）以上の結果を整理すると、点Ｈの位置を真上から見ると、三角形ＡＢＣの垂心Ｏ上にあるように見える。
（６）三角形ＡＢＣの垂心Ｏ上にある点Ｈを含む三角形ＡＢＨを辺ＡＢを中心軸にして回転させて点Ｈを回転させると、真上から見ると、点Ｈは辺ＡＢに垂直な直線Ｈ’’Ｃ上を動いて円Ｎ上の点Ｈ’’に重なる。
（７）辺ＢＣを中心にして三角形ＢＨＣを回転させて真上から見ると、点Ｈは辺ＢＣに垂直な直線ＨＡ上を動いて点Ｈに重なる。
（８）辺ＣＡを中心にして三角形ＡＣＨを回転させて真上から見ると、点Ｈは辺ＣＡに垂直な直線Ｈ’’Ｂ上を動いて点Ｈ’に重なる。
（９）そのため、求める作図は、下図のようにＡＢを直径とする円Ｎを描き、ＢＣを直径とする円Ｌを描き、ＣＡを直径とする円Ｍを描いて、三角形ＡＢＣの各頂点から対向する辺に垂直な直線を描いて作図する。
（解答おわり）
（補足）
展開図の直角三角形ＡＢＨ’’の頂点Ｈ’’と直角三角形ＢＣＨの頂点Ｈと直角三角形ＣＡＨ’の頂点Ｈが三角錐ＨＡＢＣの頂点Ｈに重なるので、
それによって、
ＡＨ’＝ＡＨ’’
ＢＨ’’＝ＢＨ
ＣＨ＝ＣＨ’
が成り立つ。
この問題を、上の３つの等式が成り立つことを証明する問題とした場合は、この展開図が三角錐ＨＡＢＣの展開図であることを証明することを介して証明すると良いと考える。
（補足２）
ＢＨ’’＝ＢＨ
を以下の計算により証明する。
先ず、ＢＨ＝ｘと置いて、
ｘを計算する。
ａ１を、以下の計算で求める。
以下の計算によって、ａ１が計算できる。
この結果を、ｘの二乗を与える式に代入する。
同様にして、ｙの二乗を計算する。
これにより、
ｙ＝ＢＨ’’＝ＢＨ＝ｘ
が証明できた。
（補足３）
ｙ＝ｘは、以下のようにして図形的に証明できる。
以上をまとめると：
よって、ｙ＝ｘ
である。
（証明おわり）
リンク：
中学数学の目次
以下は、ここをクリックした先の問題の解答です。
【問１】
上図のように、直方体ＡＢＣＤ－ＥＦＧＨがある。
ＡＢ＝１
ＢＣ＝２
ＡＥ＝１
とする。
第１の平面αと第２の平面βの成す角度を、両平面の交線上の点Ｏから、交線に対して垂直に両平面に引いた直線の間の角度であると定義する。そして、平面α側の直線が平面β側の直線に対する傾きを、平面αの平面βに対する傾きであると定義する。
図の平面ＥＢＤの、水平面ＡＢＣＤに対する傾きを求めよ。
（解答の方針）
（１）立体図形は、平面図形の問題に変換して解く。
（２）平面αと平面βの交線ＯＰに対して垂直な平面γを考える。その平面γは平面α及び平面βに垂直である。平面γと平面α及び平面βとの交線を考える。その２つの交線の間の角度が、平面αと平面βの成す角度であり、その角度が交線同士の傾き＝平面αの平面βに対する傾きを与える。
【解答】
この立体問題を簡単な形の、平面に変換して解きます。
（１）上図のように、水平面ＡＢＣＤと面ＥＢＤとの交線はＢＤです。
（２）次に、水平面ＡＢＣＤに垂直な面で、交線ＢＤに垂直な直線ＡＬを含む第２の面ＡＬＫＥを考える。
（３）第２の面ＡＬＫＥは、その面上の２つの直線ＡＬとＡＥとが交線ＢＤに垂直なので、交線に垂直な面である。また、第２の面ＡＬＫＥは長方形である。
（４）第２の面ＡＬＫＥは、 面ＥＢＤと直線ＥＰで交差する。
（５）直線ＥＰの水平線ＡＰに対する傾きが、求めるべき、平面ＥＢＤの水平面ＡＢＣＤに対する傾きである。
（６）以上の考察で、解答の道筋が分かったので、次に、詳しい計算を開始する。
上図で、線分の長さを①、②、③の順に計算した。
よって、
平面ＥＢＤの水平面ＡＢＣＤに対する傾き＝直線ＥＰの水平線ＡＰに対する傾き：
が求められた。
（解答おわり）
リンク：
中学数学の目次
以下は、ここをクリックした先の問題の解答です。
【問１】
上図のように、直方体ＡＢＣＤ－ＥＦＧＨがある。頂点Ｆから面ＥＢＧにひいた垂線の長さを求めよ。
（解答の方針）
（１）立体図形は、平面図形の問題に変換して解く。
（２）第１の面への垂線を求める問題は、第１の面上の１本の直線に垂直な第２の面を考える。その第２の面上の直線で、第１の面に垂直な直線が求める垂線である。
【解答１】
この立体問題を簡単な形の、２つの平行する面に変換して解きます。
（１）上図のように、平行する面ＥＦＧＨと面ＡＢＣＤを考える。
それら２つの面と面ＥＢＧとの交線は直線ＥＧと、それに平行な直線Ｅ’Ｇ’です。
（２）次に、面ＥＦＧＨと面ＥＢＧとが共有する１本の直線ＥＧに垂直で、点Ｆを含む第２の面ＰＦＢＱを考える。
（３）第２の面ＰＦＢＱは面ＥＦＧＨ上の直線ＥＧに垂直なので面ＥＦＧＨに垂直である。また、面ＥＢＧ上の直線ＥＧに垂直なので面ＥＢＧに垂直である。
（４）そのため、上図の第２の面ＰＦＢＱと面ＥＢＧが共有する直線ＲＢに垂直な直線ＦＳが求める垂線である。
その垂線の長さＦＳが求める長さです。
以下でその長さを計算する。
先ず、ＲＦの長さを計算する。
次に、以下の図の面ＰＦＢＱでＲＢの長さを計算した上で、ＦＳの長さを計算する。
こうして求める垂線の長さＦＳが
で求められた。
（解答おわり）
【第２の解答】高校２年生レベル
中学数学の範囲をこえるが、
下図の様に、面ＥＢＧに垂直なベクトルｈ（面の法線ベクトル）を使って垂線の長さを求める。
この係数ｂ，ｅ，ｃを以下のように計算して求める。
（補足１）
この法線ベクトルｈの計算は、（長さの違う法線ベクトルですが）以下の様に考えた方が計算の見通しが良いと考える。
この様に、面の法線ベクトルの各成分は、面の座標軸との交点の座標の逆数で計算できる。
（補足１おわり）
（補足２）
補足１と同じ長さの法線ベクトルについては、３次元の平面の式から、以下の計算によって、すぐに求められる。
点Ａを原点にした、平面ＥＢＧの３次元の平面の式は、点Bと点Eを通ることを利用すれば、点Gにかかわる未知の係数ｂを使って、以下の式であらわせる。
上の計算のように、この面が点Ｇを通ることを代入すると未知の係数ｂが－３であることが求められる。こうして面ＢＥＧをあらわす式の全ての係数が求められた。その面の式の係数が作るベクトルが法線ベクトルｈになるのである。
（補足２おわり）
式５であらわした長さの法線ベクトルの長さｈを求める。
①：点Ｄと面ＡＣＨがベクトルＡＢに平行なベクトルで隔てられ、
②：面ＡＣＨと面ＥＢＧが同じベクトルＡＢに平行なベクトルで隔てられ、
③：面ＥＢＧと点Ｆが同じベクトルＡＢに平行なベクトルで隔てられているのでそれぞれの間隔が同じである。
よって、求める垂線の長さは、ベクトルＤＦを法線ベクトルｈに射影した長さの３分の１である。
そのため、法線ベクトルｈをその長さｈで割り算して単位ベクトルにした法線ベクトルとベクトルＤＦの内積の３分の１を計算する事で垂線の長さを計算する。
ベクトルＤＦは以下の式７であらわせる。
この長さが頂点Ｆから面ＥＢＧにひいた垂線の長さである。
（解答おわり）
【第２の解答の別解（途中から）】
垂線の長さは、単位ベクトルにした法線ベクトルとベクトルEＦの内積を計算する事で求められる。
よって、式６の後は、以下の計算をすることで垂線の長さが求められる。
（解答おわり）
リンク：
中学数学の目次
高校数学の目次
上の図のような、角Ｃ直角で頂角Ａが３６°の直角三角形ＡＢＣの斜辺ＡＢの長さが１の場合に、辺ＡＣの長さを求めなさい。
上図のように、二等辺三角形ＢＤＥを考えると、その頂角∠ＤＢＥ＝３６°になります。
式２のように、ｙからｘが計算できます。
（解答おわり）
