以下は、ここをクリックした先の問題の解答です。
【問1】(これも難問だと思う)
上図の三角形ABCがある場合に、その三角形ABCを底面とする四面体で、下図のように、直方体の角Hの断片の四面体HABCを作る展開図の直角三角形の頂点H,H’,H’’を作図せよ。
【解答】
(1)図のように、辺BCを中心にして三角形BHCを回転させて真上(ABCの面に垂直な方向)から見ると、点HはBCに垂直な直線上を動くように見える。
ここで、三角形BHCは、頂角Hを直角とする直角三角形なので、辺BCを軸にして回転させると、下図のように辺BCを直径とし点Lを中心とする円L上の点Hを頂角とする直角三角形BCHに重なる。
(2)同様にして、辺ABを中心軸にして直角三角形ABHを回転させて平面ABC上に展開すると下図のように、辺ABを直径とし点Nを中心とする円N上の点H’’を頂角とする直角三角形ABH’’に重なる。
この図で、
円Lの半径=LH=LBであり、
円Nの半径=NH’’=NBであるので、
三角形NLHは三角形NLBと3辺の長さが同じで合同である。
三角形NLHを直線NLを中心軸にして回転させると、下図のように点Hが回転して点Bに重なる。
面ABCの真上から見ると、三角形NLHを直線NLを中心軸にして回転させる場合に点Hが、直線NLに垂直で点Bを通る直線上を動くように見える。
直線NLは三角形ABCの中線なので、辺ACに平行である。
それゆえ、点Hは辺ACに垂直で点Bを通る直線上を動くように見える。
(3)同様にして、点Hを別の直線を軸にして回転させて真上から見ると、以下の展開図のようになる。
三角形NMHを、直線NMを中心軸にして回転させると、点Hは回転して点Aに重なる。
真上から見ると、点Hは辺BCに平行な直線NMに垂直で点Aを通る直線AH上を動くように見える。
(4)三角形MLHを、直線MLを中心軸にして回転させると、点Hは回転して点Cに重なる。
真上から見ると、点Hは辺ABに平行な直線MLに垂直で点Cを通る直線CH’’上を動くように見える。
(5)以上の結果を整理すると、点Hの位置を真上から見ると、三角形ABCの垂心O上にあるように見える。
(6)三角形ABCの垂心O上にある点Hを含む三角形ABHを辺ABを中心軸にして回転させて点Hを回転させると、真上から見ると、点Hは辺ABに垂直な直線H’’C上を動いて円N上の点H’’に重なる。
(7)辺BCを中心にして三角形BHCを回転させて真上から見ると、点Hは辺BCに垂直な直線HA上を動いて点Hに重なる。
(8)辺CAを中心にして三角形ACHを回転させて真上から見ると、点Hは辺CAに垂直な直線H’’B上を動いて点H’に重なる。
(9)そのため、求める作図は、下図のようにABを直径とする円Nを描き、BCを直径とする円Lを描き、CAを直径とする円Mを描いて、三角形ABCの各頂点から対向する辺に垂直な直線を描いて作図する。
(解答おわり)
(補足)
展開図の直角三角形ABH’’の頂点H’’と直角三角形BCHの頂点Hと直角三角形CAH’の頂点Hが三角錐HABCの頂点Hに重なるので、
それによって、
AH’=AH’’
BH’’=BH
CH=CH’
が成り立つ。
この問題を、上の3つの等式が成り立つことを証明する問題とした場合は、この展開図が三角錐HABCの展開図であることを証明することを介して証明すると良いと考える。
(補足2)
BH’’=BH
を以下の計算により証明する。
先ず、BH=xと置いて、
xを計算する。
a1を、以下の計算で求める。
以下の計算によって、a1が計算できる。
この結果を、xの二乗を与える式に代入する。
同様にして、yの二乗を計算する。
これにより、
y=BH’’=BH=x
が証明できた。
(補足3)
y=xは、以下のようにして図形的に証明できる。
以上をまとめると:
よって、y=x
である。
(証明おわり)
リンク:
中学数学の目次
【問1】(これも難問だと思う)
上図の三角形ABCがある場合に、その三角形ABCを底面とする四面体で、下図のように、直方体の角Hの断片の四面体HABCを作る展開図の直角三角形の頂点H,H’,H’’を作図せよ。
【解答】
(1)図のように、辺BCを中心にして三角形BHCを回転させて真上(ABCの面に垂直な方向)から見ると、点HはBCに垂直な直線上を動くように見える。
ここで、三角形BHCは、頂角Hを直角とする直角三角形なので、辺BCを軸にして回転させると、下図のように辺BCを直径とし点Lを中心とする円L上の点Hを頂角とする直角三角形BCHに重なる。
(2)同様にして、辺ABを中心軸にして直角三角形ABHを回転させて平面ABC上に展開すると下図のように、辺ABを直径とし点Nを中心とする円N上の点H’’を頂角とする直角三角形ABH’’に重なる。
この図で、
円Lの半径=LH=LBであり、
円Nの半径=NH’’=NBであるので、
三角形NLHは三角形NLBと3辺の長さが同じで合同である。
三角形NLHを直線NLを中心軸にして回転させると、下図のように点Hが回転して点Bに重なる。
面ABCの真上から見ると、三角形NLHを直線NLを中心軸にして回転させる場合に点Hが、直線NLに垂直で点Bを通る直線上を動くように見える。
直線NLは三角形ABCの中線なので、辺ACに平行である。
それゆえ、点Hは辺ACに垂直で点Bを通る直線上を動くように見える。
(3)同様にして、点Hを別の直線を軸にして回転させて真上から見ると、以下の展開図のようになる。
三角形NMHを、直線NMを中心軸にして回転させると、点Hは回転して点Aに重なる。
真上から見ると、点Hは辺BCに平行な直線NMに垂直で点Aを通る直線AH上を動くように見える。
(4)三角形MLHを、直線MLを中心軸にして回転させると、点Hは回転して点Cに重なる。
真上から見ると、点Hは辺ABに平行な直線MLに垂直で点Cを通る直線CH’’上を動くように見える。
(5)以上の結果を整理すると、点Hの位置を真上から見ると、三角形ABCの垂心O上にあるように見える。
(6)三角形ABCの垂心O上にある点Hを含む三角形ABHを辺ABを中心軸にして回転させて点Hを回転させると、真上から見ると、点Hは辺ABに垂直な直線H’’C上を動いて円N上の点H’’に重なる。
(7)辺BCを中心にして三角形BHCを回転させて真上から見ると、点Hは辺BCに垂直な直線HA上を動いて点Hに重なる。
(8)辺CAを中心にして三角形ACHを回転させて真上から見ると、点Hは辺CAに垂直な直線H’’B上を動いて点H’に重なる。
(9)そのため、求める作図は、下図のようにABを直径とする円Nを描き、BCを直径とする円Lを描き、CAを直径とする円Mを描いて、三角形ABCの各頂点から対向する辺に垂直な直線を描いて作図する。
(解答おわり)
(補足)
展開図の直角三角形ABH’’の頂点H’’と直角三角形BCHの頂点Hと直角三角形CAH’の頂点Hが三角錐HABCの頂点Hに重なるので、
それによって、
AH’=AH’’
BH’’=BH
CH=CH’
が成り立つ。
この問題を、上の3つの等式が成り立つことを証明する問題とした場合は、この展開図が三角錐HABCの展開図であることを証明することを介して証明すると良いと考える。
(補足2)
BH’’=BH
を以下の計算により証明する。
先ず、BH=xと置いて、
xを計算する。
a1を、以下の計算で求める。
以下の計算によって、a1が計算できる。
この結果を、xの二乗を与える式に代入する。
同様にして、yの二乗を計算する。
これにより、
y=BH’’=BH=x
が証明できた。
(補足3)
y=xは、以下のようにして図形的に証明できる。
以上をまとめると:
よって、y=x
である。
(証明おわり)
リンク:
中学数学の目次













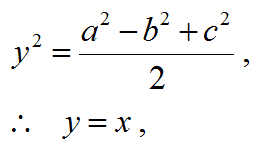





0 件のコメント:
コメントを投稿