以下は、ここをクリックした先の問題の解答です。
【問1】(難問)
上の図のような、角C直角で頂角Aが36°の直角三角形ABCの斜辺ABの長さが1の場合に、辺ACの長さを求めなさい。
《解答手順》
図形問題では、先ず、足りない図形の補助線を埋め込み、同じ角度には同じ印を付け、なるべく対称な形に、図形を完成させる。その次に問題の解き方を考えるように心がけてください。
【解答】
まず、以下の様に、36°の頂角Aを頂角にする二等辺三角形ABDを考えます。
上図のように、二等辺三角形BDEを考えると、その頂角∠DBE=36°になります。
そのため、
△ABD∽△BDE
です。
また、∠ABE=36°=∠BAE
ですので、
△EABは二等辺三角形になり、
AE=EB
です。
また、
EB=DB=y
です。
そのため、以下の図の式1と式2が得られます。
式2のように、yからxが計算できます。
そのため、yの式1を解けば良いことがわかります。
(解答おわり)
リンク:
中学数学の目次
【問1】(難問)
《解答手順》
図形問題では、先ず、足りない図形の補助線を埋め込み、同じ角度には同じ印を付け、なるべく対称な形に、図形を完成させる。その次に問題の解き方を考えるように心がけてください。
【解答】
まず、以下の様に、36°の頂角Aを頂角にする二等辺三角形ABDを考えます。
そのため、
△ABD∽△BDE
です。
また、∠ABE=36°=∠BAE
ですので、
△EABは二等辺三角形になり、
AE=EB
です。
また、
EB=DB=y
です。
そのため、以下の図の式1と式2が得られます。
式2のように、yからxが計算できます。
そのため、yの式1を解けば良いことがわかります。
(解答おわり)
リンク:
中学数学の目次


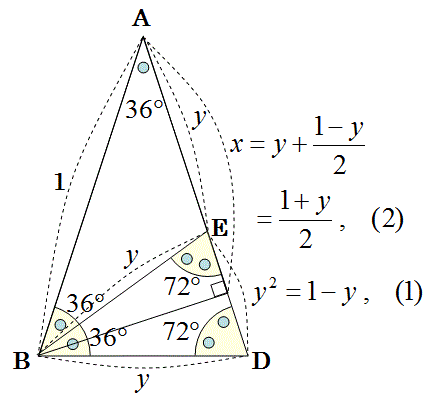

0 件のコメント:
コメントを投稿