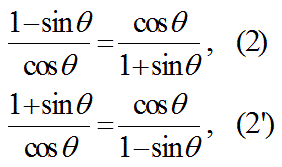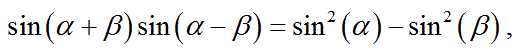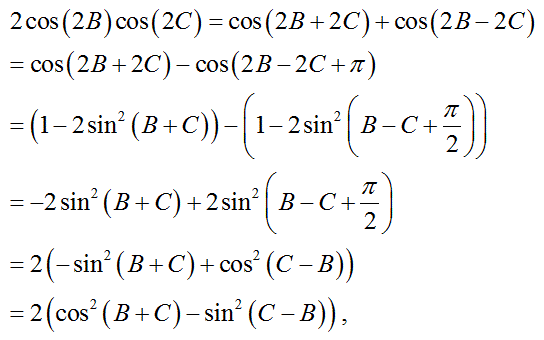これは、ここをクリックした先のページの問題の解答です。
【公式１】
分数式の分母が０になる場合を除き、
以下の式１及び１’：
が成り立つ事を証明せよ。
【証明開始】
式１又は式１’を変形する：
この計算を逆にたどることで式１が得られる。
（証明おわり）
【公式２】
分数式の分母が０になる場合を除き、
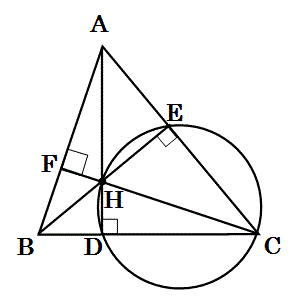
以下の式２及び２’：
が成り立つ事を証明せよ。
【証明開始】
式２又は式２’を変形する：
この計算を逆にたどることで式２が得られる。
（証明おわり）
【公式３】
分数式の分母が０になる場合を除き、
以下の式４：
及び、
が成り立つ事を証明せよ。
【証明開始】
式４又は式４’を変形する：
この計算を逆にたどることで式４が得られる。
（証明おわり）
（補足）
この式４は、以下の図からも求める事ができる。
しかし、この図から式４を導き出すよりも、先の証明の計算の方が楽に式４を導き出すことができます。
【公式４】
分数式の分母が０になる場合を除き、
以下の式５：
及び、
が成り立つ事を証明せよ。
【証明開始】
式５又は式５’を変形する：
この計算を逆にたどることで式５が得られる。
（証明おわり）
（補足）
式５は、以上の様に証明できましたが、そもそも、式５のＣを（（π／２）ーθ）に置き換えれば、ｃｏｓＣ→ｓｉｎθに変わり、ｓｉｎＣ→ｃｏｓθに変わり、式５は、式４の形の式に変わります。
そのように角度Ｃの変数の置換えをするならば、式５の形は式４の形に変換できるので、式５を考える必要がありません。
リンク：
高校数学の目次
これは、ここをクリックした先の問題の解答です。
【問１】
上図のように、ＸＹ座標軸の原点Ｏを頂点にする二等辺三角形ＯＡＢがあり、
ＯＡ＝ＯＢ
である。
辺ＡＢの中点をＭとする。
ＭからＹ軸に平行に引いた直線と、
ＢからＸ軸に平行に引いた直線の交点をＮとする。
ＭからＹ軸に引いた垂線の足をＱとする。
Ｂから辺ＯＡに引いた垂線の足をＨとする。
このとき、
三角形ＱＭＮと三角形ＢＨＡが相似であることを証明せよ。
【証明開始】
ＭＯ⊥ ＭＢ
である。
また、
ＭＱ⊥ＭＮ
である。
よって、
△ＯＭＱ∽△ＢＭＮ
よって、
よって
△ＱＭＮと△ＯＭＢ
の直角をはさむ２辺の比が等しい。
また、△ＱＭＮと△ＯＭＢはいずれも直角三角形であって、１つの角度が直角で等しい。
２辺の比が等しく、その２辺の間の角度が等しいので、
△ＱＭＮ∽△ＯＭＢ （１）
△ＯＭＢと△ＢＨＡは、
∠ＯＢＭ＝∠ＢＡＨ
であり、あと１つの角度が直角で等しい。
よって、２角が等しいので、
△ＯＭＢ∽△ＢＨＡ （２）
（１）と（２）より、
これは、ここをクリックした先のページの問題の解答です。
【公式１】
分数式の分母が０になる場合を除き、
以下の式：
が成り立つ事を証明せよ。
なお、角度ＣをーＣに置き換えれば、式１は：
になる。
更に角度Ｃを（π／２）ーＣに置き換えれば、式２は：
になる。
（補足）
式３の左辺の形を見たら、式３のＣを（（π／２）ーθ）に置き換えれば、ｃｏｓＣ→ｓｉｎθに変わり、ｓｉｎＣ→ｃｏｓθに変わり、式３は、式２の形の式に変わります。
そのように角度Ｃの変数の置換えをするならば、式３の形は式２の形に変換できるので、式３を考える必要がありません。
【証明開始】
式１の中間の辺を以下のように変形する。
（式１の左辺＝中間の辺の証明おわり）
（式１の中間の辺＝右辺の証明おわり）
（証明おわり）
（補足）
この公式１は、下図において：
ＭＮ／ＭＱ＝ＨＣ／ＨＢ
の関係がある事を示している。
それは、
△ＭＮＱ∽△ＨＣＢ
であるので、
成り立っている。
（ここをクリックした先の問題を参照してください）
【公式２】
分数式の分母が０になる場合を除き、
以下の式４：
及び、
が成り立つ事を証明せよ。
【証明開始】
式４又は式４’を変形する：
この計算を逆にたどることで式４が得られる。
（証明おわり）
【公式３】
分数式の分母が０になる場合を除き、
以下の式５：
及び、
が成り立つ事を証明せよ。
【証明開始】
式５又は式５’を変形する：
この計算を逆にたどることで式５が得られる。
（証明おわり）
（補足）
式５は、以上の様に証明できましたが、そもそも、式５のＣを（（π／２）ーθ）に置き換えれば、ｃｏｓＣ→ｓｉｎθに変わり、ｓｉｎＣ→ｃｏｓθに変わり、式５は、式４の形の式に変わります。
そのように角度Ｃの変数の置換えをするならば、式５の形は式４の形に変換できるので、式５を考える必要がありません。
【公式４】
分数式の分母が０になる場合を除き、
以下の式６：
及び式７：
が成り立つ事を証明せよ。
【証明開始】
式６は、以下の計算で証明できる。
式７は、以下の計算で証明できる。
（証明おわり）
リンク：
高校数学の目次
これは、ここをクリックした先の問題の解答です。
【問１】
上図の角度の関係、すなわち、
三角形の垂心Ｈの周りの角度が、上図の様に、三角形の頂角と同じ角度になっていることを証明せよ。
【第１の証明開始】
先ず、下図で考える。
三角形ＢＣＥと三角形ＢＨＤは、
(1)頂角Ｂが同じ角度で、
(2)もう１つの頂角が
∠ＢＥC＝∠ＢＤＨ＝９０°
であって同じなので、
(3)三角形は相似になり
△ＢＣＥ∽△ＢＨＤ
∴ ∠ＢＣＥ＝∠ＢＨＤ＝∠Ｃ
同様にして、
△ ＣＡＦ∽△ＣＨＥ
∴ ∠ＣＡＦ＝∠ＣＨＥ＝∠Ａ
同様にして、
△ ＡＢＤ∽△ＡＨＦ
∴ ∠ＡＢＤ＝∠ＡＨＦ＝∠Ｂ
（証明おわり）
【第２の証明開始】
下図のように、三角形ＨＣＥの外接円を考える。
この外接円に内接する三角形ＥＨＣは、頂角Ｅが直角な三角形であるため、
辺ＨＣは外接円の直径になる。
その外接円の辺ＨＣの上側の円周角が９０°であるので、
辺ＨＣの下側の円周角は、
１８０°－９０°＝９０°
である。
そのため、下側の円周角と等しい直角の頂角Ｄを持つ直角三角形ＨＣＤも
その外接円に内接する。
∴ 四辺形ＥＨＤＣは三角形ＥＨＣの外接円に内接する。
拡張円周角の定理により、
三角形ＡＢＣの∠Ｃと同じ角度が点Ｈの周りの下図の位置にある。
外接円を除去して書くと以下の図になる。
同様にして、三角形ＡＢＣの他の頂角Ａ、頂角Ｂも点Ｈの周囲の、下図の位置にある。
（証明おわり）
リンク：
中学数学の目次
高校数学の目次
【証明開始】
左辺の２倍を以下のように変形する。
（証明おわり）
【複素数平面を使った証明】
上図の様に、複素数ｚとｗを定義する。
である。
ｚとｗを使って問題の等式を式１に書き変える。
この式１の左辺と右辺のそれぞれを計算する。
式１の左辺は：
式１の右辺は：
式２と式３は等しい。
よって式１が成り立つ。
よって公式１が成り立つ。
（証明おわり）
（補足）
このように。複素数平面で計算できるようになれば、三角関数の加法定理や三角関数の和と積の公式を忘れても、それらの公式を使う問題を解くことができるようになります。
【公式２】
角度Ｂと角度Ｃに関して、以下の式：
又は、
又は、
が成り立つ事を証明せよ。
【証明開始】
左辺の２倍を以下のように変形する。
（証明おわり）
リンク：
高校数学の目次
が成り立つ事を証明せよ。
この計算を逆にたどることで式１が得られる。
が成り立つ事を証明せよ。
この計算を逆にたどることで式２が得られる。
及び、
が成り立つ事を証明せよ。
この計算を逆にたどることで式４が得られる。
しかし、この図から式４を導き出すよりも、先の証明の計算の方が楽に式４を導き出すことができます。 
及び、
が成り立つ事を証明せよ。
この計算を逆にたどることで式５が得られる。
