【証明開始】
左辺の2倍を以下のように変形する。
(証明おわり)
【複素数平面を使った証明】
上図の様に、複素数zとwを定義する。
である。
zとwを使って問題の等式を式1に書き変える。
この式1の左辺と右辺のそれぞれを計算する。
式1の左辺は:
式1の右辺は:
式2と式3は等しい。
よって式1が成り立つ。
よって公式1が成り立つ。
(証明おわり)
(補足)
このように。複素数平面で計算できるようになれば、三角関数の加法定理や三角関数の和と積の公式を忘れても、それらの公式を使う問題を解くことができるようになります。
【公式2】
角度Bと角度Cに関して、以下の式:
又は、 が成り立つ事を証明せよ。
【証明開始】
左辺の2倍を以下のように変形する。
リンク:
高校数学の目次

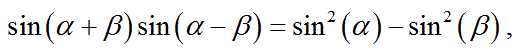










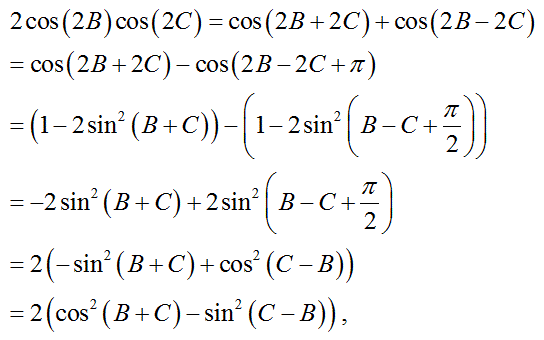
0 件のコメント:
コメントを投稿