これは、ここをクリックした先のページの問題の解答です。
【公式1】
分数式の分母が0になる場合を除き、
以下の式1及び1’:
が成り立つ事を証明せよ。
【証明開始】
式1又は式1’を変形する:
この計算を逆にたどることで式1が得られる。
(証明おわり)
【公式2】
分数式の分母が0になる場合を除き、
以下の式2及び2’:
が成り立つ事を証明せよ。
【証明開始】
式2又は式2’を変形する:
この計算を逆にたどることで式2が得られる。
(証明おわり)
【公式3】
分数式の分母が0になる場合を除き、
以下の式4:
及び、
が成り立つ事を証明せよ。
【証明開始】
式4又は式4’を変形する:
この計算を逆にたどることで式4が得られる。
(証明おわり)
(補足)
この式4は、以下の図からも求める事ができる。
しかし、この図から式4を導き出すよりも、先の証明の計算の方が楽に式4を導き出すことができます。
【公式4】
分数式の分母が0になる場合を除き、
以下の式5:
及び、
が成り立つ事を証明せよ。
【証明開始】
式5又は式5’を変形する:
この計算を逆にたどることで式5が得られる。
(証明おわり)
(補足)
式5は、以上の様に証明できましたが、そもそも、式5のCを((π/2)ーθ)に置き換えれば、cosC→sinθに変わり、sinC→cosθに変わり、式5は、式4の形の式に変わります。
そのように角度Cの変数の置換えをするならば、式5の形は式4の形に変換できるので、式5を考える必要がありません。
リンク:
高校数学の目次
【公式1】
分数式の分母が0になる場合を除き、
以下の式1及び1’:
が成り立つ事を証明せよ。
【証明開始】
式1又は式1’を変形する:
この計算を逆にたどることで式1が得られる。
(証明おわり)
【公式2】
分数式の分母が0になる場合を除き、
以下の式2及び2’:
【証明開始】
式2又は式2’を変形する:
(証明おわり)
【公式3】
分数式の分母が0になる場合を除き、
以下の式4:
及び、
が成り立つ事を証明せよ。
【証明開始】
式4又は式4’を変形する:
この計算を逆にたどることで式4が得られる。
(証明おわり)
(補足)
この式4は、以下の図からも求める事ができる。
しかし、この図から式4を導き出すよりも、先の証明の計算の方が楽に式4を導き出すことができます。
【公式4】
分数式の分母が0になる場合を除き、
以下の式5:
及び、
が成り立つ事を証明せよ。
【証明開始】
式5又は式5’を変形する:
この計算を逆にたどることで式5が得られる。
(証明おわり)
(補足)
式5は、以上の様に証明できましたが、そもそも、式5のCを((π/2)ーθ)に置き換えれば、cosC→sinθに変わり、sinC→cosθに変わり、式5は、式4の形の式に変わります。
そのように角度Cの変数の置換えをするならば、式5の形は式4の形に変換できるので、式5を考える必要がありません。
リンク:
高校数学の目次


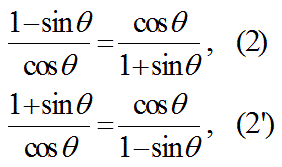








0 件のコメント:
コメントを投稿