三角形の垂心の周りの角度

これは、ここをクリックした先の問題の解答です。

【問１】 

上図の角度の関係、すなわち、
三角形の垂心Ｈの周りの角度が、上図の様に、三角形の頂角と同じ角度になっていることを証明せよ。

【第１の証明開始】
先ず、下図で考える。

三角形ＢＣＥと三角形ＢＨＤは、
(1)頂角Ｂが同じ角度で、
(2)もう１つの頂角が
∠ＢＥC＝∠ＢＤＨ＝９０°
であって同じなので、
(3)三角形は相似になり
△ＢＣＥ∽△ＢＨＤ
∴　∠ＢＣＥ＝∠ＢＨＤ＝∠Ｃ

同様にして、
△ ＣＡＦ∽△ＣＨＥ
∴　∠ＣＡＦ＝∠ＣＨＥ＝∠Ａ

同様にして、
△ ＡＢＤ∽△ＡＨＦ
∴　∠ＡＢＤ＝∠ＡＨＦ＝∠Ｂ

（証明おわり）

【第２の証明開始】
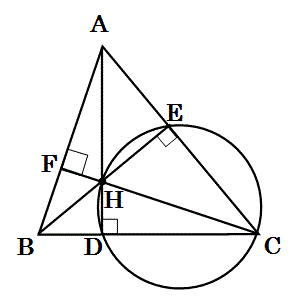
下図のように、三角形ＨＣＥの外接円を考える。

この外接円に内接する三角形ＥＨＣは、頂角Ｅが直角な三角形であるため、
辺ＨＣは外接円の直径になる。

その外接円の辺ＨＣの上側の円周角が９０°であるので、
辺ＨＣの下側の円周角は、
１８０°－９０°＝９０°
である。
そのため、下側の円周角と等しい直角の頂角Ｄを持つ直角三角形ＨＣＤも
その外接円に内接する。
∴　四辺形ＥＨＤＣは三角形ＥＨＣの外接円に内接する。

拡張円周角の定理により、
三角形ＡＢＣの∠Ｃと同じ角度が点Ｈの周りの下図の位置にある。

外接円を除去して書くと以下の図になる。

 同様にして、三角形ＡＢＣの他の頂角Ａ、頂角Ｂも点Ｈの周囲の、下図の位置にある。

（証明おわり）

【問２】
　以下の三角形ＡＢＣに外接する円と直線ＡＤとの交点Ｊの周りの角度が図のようになることを証明せよ。


【証明開始】
弦ＡＣに関する円周角が等しいので、
∠ＡＪＣ＝∠ＡＢＣ＝∠Ｂ，
弦ＡＢに関する円周角が等しいので、
∠ＡＪＢ＝∠ＡＣＢ＝∠Ｃ，
（証明おわり）

【問３】
　問２の３角形に関して、
ＡＤ×ＨＤ＝ＢＤ×ＣＤ
が成り立つことを証明せよ。

【証明開始】
　三角形ＨＢＤと三角形ＪＢＤに関して、
３角が等しい。
かつ、辺ＢＤが共通で対応する辺の長さが等しい。
よって、二角夾辺が等しいので、三角形ＨＢＤと三角形ＪＢＤは合同である。
そのため、
ＨＤ＝ＪＤ
である。
一方で、円の方べきの定理により、
ＪＤ×ＤＡ＝ＢＤ×ＣＤ
ゆえに、
ＡＤ×ＨＤ＝ＢＤ×ＣＤ
（証明おわり）

リンク：
中学数学の目次
高校数学の目次