⊿ＡＢＣの面積Ｓの公式の導き方

これは、ここをクリックした先の問題の解答です。

【問０】⊿ＡＢＣの面積Ｓを⊿ＡＢＣの３辺ａ，ｂ，ｃと⊿ＡＢＣの外接円の半径Ｒであらわす公式を求めよ。

　この問題をもっとやさしい問題に変換して解きます。

【問１】以下の直角三角形⊿ＡＢＣの面積Ｓを⊿ＡＢＣの３辺ａ，ｂ，ｃと⊿ＡＢＣの外接円の半径Ｒであらわせ。

このように簡単化した問題は、すぐ上の式であらわした解があります。

　もう１つのやさしい問題を解きます。

【問２】以下の直角三角形⊿ＡＢＣの面積Ｓを⊿ＡＢＣの３辺ａ，ｂ，ｃと⊿ＡＢＣの外接円の半径Ｒであらわせ。

このように簡単化した問題は、すぐ上の式であらわした解があります。

この２つの公式を、もっと一般的な形の三角形に関する１つの公式の一部があらわれた公式であると考えます。

（ａとｂが直角三角形の２辺ならば、残りの辺ｃは、直径＝２Ｒに等しくなり、ｃ／（２Ｒ）＝１になっています）
上の式のように、問１と問２との、特殊な形に対して成り立つ公式を、一般的な形に対して１つの式であらわすとどうなるかを考えます。
　この式が求める公式のようだと見当がつきました。
　こうして答えが何になるかの見当を付ける思考実験をするように心がけましょう。答えの見当が付くと、安心してリラックスでき、心に余裕ができます。この余裕がとても大切です。

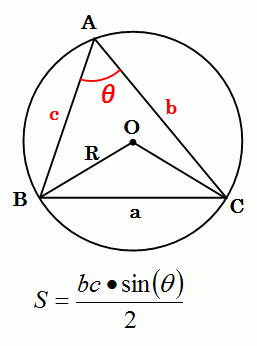
　次に、この２つの式を、もう少し一般的な形の三角形について厳密に計算してみようと、以下のような計算の試みをしてみます。

この式が求める公式と違う点は、角度θに関するsinの式が入っているのが余分で、ａとＲの式が無いことです。
この余分なsinの式を、不足しているａとＲの式であらわせないかと考えます。

そして、そのsinの式をａとＲの式であらわす式（正弦定理）の証明方法を思い出して、上の正弦定理の式を導き出します。
　この式を、以下のようにして先の式に代入して、余分な角度θに関するsinの式を、ａとＲの式に置き換えます。

こうして、公式を導き出すことに成功しました。
　この結果の答えが面白いのでおぼえておいても良いですが、
答えをおぼえるよりは、この解き方の方がおぼえやすいと思います。

リンク：
高校数学の目次