
【解答】
式1を以下のように変形して式2を求める。

この式2が無限に大きいxとyとで成り立ち得るか否かを考える。それが成り立たなければ、この式2で表される図形は双曲線にはならず、楕円である。
よって、以下の式で図形の形が判別できる。

(解答おわり)
【問2】
原点の回りに回転させた楕円の方程式から楕円の軸を計算せよ。
すなわち、回転した楕円の方程式を、位置ベクトルに対するべクトルの関数Fを使って、以下の式であらわしたとき。

このように、系数A,B,Cを使ったX座標とY座標の関数で楕円があらわされたとき、
そのベクトル関数Fは、X座標の方向の単位ベクトルxと、Y座標の方向の単位ベクトルyを、系数A,B,Cを使った以下の式で新たなベクトルに変換する関数であると考えることができる。
このベクトル関数によってベクトルの方向が変えられないベクトルgとhは、以下の図であらわすように、回転した楕円の軸方向のベクトルを表わしていると考えられる。
その軸方向のベクトルgとhの、x座標軸と成す角度θのタンジェントtanθを求めよ。
【解答】
そのベクトルg(又はh)を以下の式であらわし、以下のベクトル方程式を作る。
ここで、ベクトルgとhは、ベクトル関数Fによって方向が変えられず、それぞれ異なる倍率λ倍に長さが拡大される。
そのように関数Fによって方向が変わらないベクトルg(又はh)を以下のようにベクトル方程式を設定することで求める。
上の連立方程式が得られた。
この式がX=Y=0以外のXとYの解を持つためには以下の式が成り立つ必要がある。
ここで、Y/Xは求めるtanθである。λの値が求められるとtanθの値も求めることができる。
λを以下のように計算しtanθを計算する。
これでtanθが計算できた。
これによりベクトルgとhの角度θがわかったのであるが、
この答えが正しいかどうかを以下にように検算する。
ベクトルgとhは互いに垂直であるので、この答えでベクトルgとhの内積を計算して、それが0になるかどうかを確認する。

上の計算で、たしかに、ベクトルgとhの内積は0になり、両ベクトルが直交することが確認できた。
(補足)
以下で計算した結果の、tan(2θ)をA,B,Cであらわす式は覚えやすい形をしている。
(補足2)
この式は、A,B,Cを定義した式(設問以前の解説を参照)から、以下のようにして導き出すこともできました。
(補足3)
この問題は、グラフをあらわす式の1/b2を-1/b2に置き換えたグラフに対しても使える解き方です。すなわち、双曲線をあらわす式に対しても、その双曲線の軸ベクトルを求める方法としても使えます。
(補足4)
楕円の軸の回転角度θを与えるこの式は、何度おぼえても忘れます。その忘れ対策として、この式を以下の様にして素早く導き出しましょう。
(回転した楕円の式の係数2Bは、以下の計算ではBとしています。以下では、係数Bの定義が異なることに注意。)
先ず、上の図を思い描きます。
極座標で表した動径rが最大または最小になる角度α=θです。
そのため、以下のようにして動径rの微分の式を作ります。
この式2の微分をf(α)の式に行います。
この式4が求める回転角θを与える式です。
リンク:
高校数学の目次
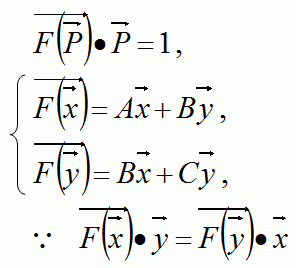













0 件のコメント:
コメントを投稿