これは、ここをクリックした先の問題の解答です。
【問0】三角形の垂心Oの位置ベクトルをもとめよ。
この問題をもっと易しい問題に変換して解きます。
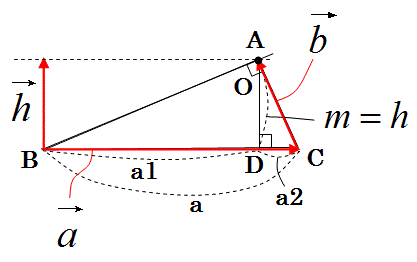
【問1】以下の直角三角形の垂心Oの位置ベクトルをもとめよ。
このように簡単化した問題は、すぐ上の式であらわしたベクトルDOの長さmの解
m=h
があります。
もう1つのやさしい問題を解きます。
【問2】以下の直角三角形の垂心Oの位置ベクトルをもとめよ。
このようにベクトルDOの長さmが0になる条件が成り立っている場合では、その条件の場合に値が0になる辺a1とa2の積の項と他の何かの項(?)の積でベクトルDOの公式を推測します。他の何かの項(?)は未だ分からないでも良いと判断します。
次に、問1の条件が成り立っている時に、問2で推測したベクトルDOの長さmの公式が問2で得た解に等しくなるように、他の何かの項(?)を定めて以下の式を求めました。
こうして、上の式のように、ベクトルDOの長さmの公式をハッキリした式で推測しました。
また、この推測の結果は、この公式を導き出すための基準にするベクトルはベクトルaとそれに垂直なベクトルを基準にしたら良いと示唆するという重要な指針(計算のガイド)を含んでいます。
これで得た公式は推測であって、本当にこの式になるかの確証があるわけではありません。
しかし、これで、公式の答えを予測できたので、正式な計算で公式を計算する道しるべができたという意味があります。
このように、答えを予測する計算は、初めて未知の問題を解くときに大切な一歩であり、必要な計算です。是非、答えの予測計算を心がけて欲しいと思います。
次に、正式な計算方法でこの公式を求めます。
【一番簡単な解き方の秘訣】
(あるベクトルmとcとが互いに垂直であるという条件のある図形の問題を解くときは、
(1)それらのベクトルmとcを、互いに垂直な単位ベクトルxとyの合成であらわして(ただし、ベクトルxは、三角形の所定の辺の方向に平行。ベクトルyはその辺に垂直な方向を向く)、
(2)そして、ベクトルmとcが垂直である条件として内積が0であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。)
以下の図のような三角形を考えて、ベクトル方程式を解いてベクトルDOの長さmの公式を計算します。
ここで、互いに直交するベクトルxとyと未知数mでベクトルDOをあらわす。このときベクトルBOは上の式であらわせる。
ベクトルBOとベクトルbが直交するベクトル方程式を作って、それを解きます。
このmの式の形を整えるにあたって、先に予測した式になっているかを確かめながら、予測した式になるように式を変形しました。
その結果、予測通りの式が得られました。
この結果を使って、ベクトルDOの長さmが以下の図のようにあらわせます。
(計算を振り返ってどこが良かったかを考える)
以上の計算で大事なポイントは、先に公式の解の形を予測してから正式な計算に取りかかった事でした。答えを予測してから正式な計算をしたことで、正式な計算が、「本当に予測通りの答えを導き出せるのか」という期待に背中を押されて計算できました。
そして、式を計算していく過程で、どういう形の式に答えを導くべきかの目標がはっきりしているので、式を何に置き換えてまとめ上げるかの道に迷わず、答えを得ることができました。
すなわち、先に予測していた事が、式を次にどのような形に変形したら良いかというガイドになりました。
このガイドが無ければ、式の計算が最後の形にまで変形できなかったかもしれませんので、先に行なった解の推測の計算がとても大切な役割を果たしました。
特に、先に行なった解の推測の計算は、問題を解くために、どのベクトルを基準にしたら良いかを示唆するという重要な指針を含んでいますので、問題を解くためにとても大切な役割を持っていました。
【補足】
以上の計算結果を使って、三角形の上の頂点から垂心までの距離(h-m)を計算してみます。
この式で計算した長さ(h-m)の値は、三角形の底辺の上の外心の高さの2倍です。
この式を変形して以下の形の公式をあらわすことができる。


リンク:
2直線の関係(三角形の外接円の中心の座標)
高校数学の目次
【問0】三角形の垂心Oの位置ベクトルをもとめよ。
【問1】以下の直角三角形の垂心Oの位置ベクトルをもとめよ。
m=h
があります。
もう1つのやさしい問題を解きます。
【問2】以下の直角三角形の垂心Oの位置ベクトルをもとめよ。
次に、問1の条件が成り立っている時に、問2で推測したベクトルDOの長さmの公式が問2で得た解に等しくなるように、他の何かの項(?)を定めて以下の式を求めました。
また、この推測の結果は、この公式を導き出すための基準にするベクトルはベクトルaとそれに垂直なベクトルを基準にしたら良いと示唆するという重要な指針(計算のガイド)を含んでいます。
これで得た公式は推測であって、本当にこの式になるかの確証があるわけではありません。
しかし、これで、公式の答えを予測できたので、正式な計算で公式を計算する道しるべができたという意味があります。
このように、答えを予測する計算は、初めて未知の問題を解くときに大切な一歩であり、必要な計算です。是非、答えの予測計算を心がけて欲しいと思います。
次に、正式な計算方法でこの公式を求めます。
【一番簡単な解き方の秘訣】
(あるベクトルmとcとが互いに垂直であるという条件のある図形の問題を解くときは、
(1)それらのベクトルmとcを、互いに垂直な単位ベクトルxとyの合成であらわして(ただし、ベクトルxは、三角形の所定の辺の方向に平行。ベクトルyはその辺に垂直な方向を向く)、
(2)そして、ベクトルmとcが垂直である条件として内積が0であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。)
以下の図のような三角形を考えて、ベクトル方程式を解いてベクトルDOの長さmの公式を計算します。
ここで、互いに直交するベクトルxとyと未知数mでベクトルDOをあらわす。このときベクトルBOは上の式であらわせる。
ベクトルBOとベクトルbが直交するベクトル方程式を作って、それを解きます。
その結果、予測通りの式が得られました。
この結果を使って、ベクトルDOの長さmが以下の図のようにあらわせます。
(計算を振り返ってどこが良かったかを考える)
以上の計算で大事なポイントは、先に公式の解の形を予測してから正式な計算に取りかかった事でした。答えを予測してから正式な計算をしたことで、正式な計算が、「本当に予測通りの答えを導き出せるのか」という期待に背中を押されて計算できました。
そして、式を計算していく過程で、どういう形の式に答えを導くべきかの目標がはっきりしているので、式を何に置き換えてまとめ上げるかの道に迷わず、答えを得ることができました。
すなわち、先に予測していた事が、式を次にどのような形に変形したら良いかというガイドになりました。
このガイドが無ければ、式の計算が最後の形にまで変形できなかったかもしれませんので、先に行なった解の推測の計算がとても大切な役割を果たしました。
特に、先に行なった解の推測の計算は、問題を解くために、どのベクトルを基準にしたら良いかを示唆するという重要な指針を含んでいますので、問題を解くためにとても大切な役割を持っていました。
【補足】
以上の計算結果を使って、三角形の上の頂点から垂心までの距離(h-m)を計算してみます。
この式で計算した長さ(h-m)の値は、三角形の底辺の上の外心の高さの2倍です。
この式を変形して以下の形の公式をあらわすことができる。


リンク:
2直線の関係(三角形の外接円の中心の座標)
高校数学の目次

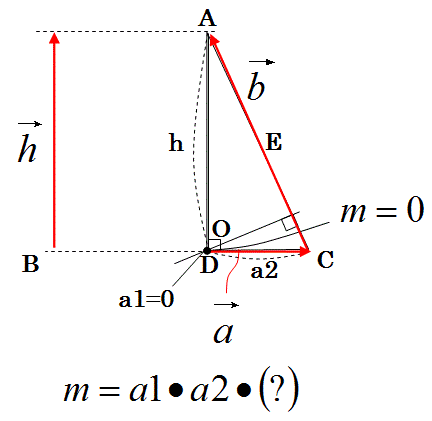





0 件のコメント:
コメントを投稿