三角形の垂心の位置ベクトルをあらわす元のベクトルを何にするか

これは、ここをクリックした先の問題の解答です。

ページ内リンク：
▽解の推測の計算
▽一番簡単な解き方の秘訣
▽第１の解
▽解の変形
▽第２の解

【問０】三角形の垂心Ｏの位置ベクトルをもとめよ。

　この問題をもっと易しい問題に変換して解きます。

【問１】以下の直角三角形の垂心Ｏの位置ベクトルをもとめよ。

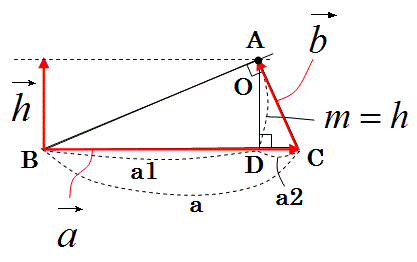
このように簡単化した問題は、すぐ上の式であらわしたベクトルＤＯの長さｍの解
ｍ＝ｈ
があります。

　もう１つのやさしい問題を解きます。

【問２】以下の直角三角形の垂心Ｏの位置ベクトルをもとめよ。

このようにベクトルＤＯの長さｍが０になる条件が成り立っている場合では、その条件の場合に値が０になる辺ａ１とａ２の積の項と他の何かの項（？）の積でベクトルＤＯの公式を推測します。他の何かの項（？）は未だ分からないでも良いと判断します。

　次に、問１の条件が成り立っている時に、問２で推測したベクトルＤＯの長さｍの公式が問２で得た解に等しくなるように、他の何かの項（？）を定めて以下の式を求めました。

こうして、上の式のように、ベクトルＤＯの長さｍの公式をハッキリした式で推測しました。
　また、この推測の結果は、この公式を導き出すための基準にするベクトルはベクトルａとそれに垂直なベクトルを基準にしたら良いと示唆するという重要な指針（計算のガイド）を含んでいます。
 
　これで得た公式は推測であって、本当にこの式になるかの確証があるわけではありません。
　しかし、これで、公式の答えを予測できたので、正式な計算で公式を計算する道しるべができたという意味があります。
　このように、答えを予測する計算は、初めて未知の問題を解くときに大切な一歩であり、必要な計算です。是非、答えの予測計算を心がけて欲しいと思います。

　次に、正式な計算方法でこの公式を求めます。
 
【一番簡単な解き方の秘訣】
　（あるベクトルＢＯとｂが互いに垂直であるという条件のある図形の問題を解くときは、
（１）それらのベクトルＢＯとｂを、互いに垂直な単位ベクトルｘとｙの合成であらわして、
（２）そして、ベクトルＢＯとｂが垂直である条件として内積が０であるというベクトル方程式を作って計算すると、
計算が一番簡単になります。）

【第１の解】
　ここでは、この一番簡単な解の秘訣に従わないで、問題を解いてみます。すなわち、ここでは、「（１）それらのベクトルＢＯとｂを、互いに垂直な単位ベクトルｘとｙの合成であらわす」ことをしないで、ベクトルＢＯを互いに垂直とは限らないベクトルａとｂであらわして問題を解いてみます。

　つまり、先に行なった予測計算の結果が示唆している、「基準にするベクトルとして、 ベクトルａとそれに垂直なベクトルを基準にしたら良いという重要な示唆」をあえて無視してみます。 

≪この示唆を無視しない解き方は、ここをクリックした先にあります≫

（単位ベクトルを使わずとも、ベクトルａとそれに垂直な何かのベクトルを使うだけで解答がし易くなりますが、それもしないことにします）

　以下の図のような三角形を考えて、ベクトル方程式を解いてベクトルＤＯの長さｍの公式を計算します。

ここで、ベクトルａとｂを元ベクトルにして上の式のようにベクトルＢＯをあらわすことにする。
この答えはどの様になるか、以下で調べます。

ベクトルＢＯとベクトルｂが直交するベクトル方程式と、ベクトルＡＯとベクトルａが直交するベクトル方程式を作ります。

　以下でこの連立ベクトル方程式を解いて変数ｓとｔを計算します。

（第１の解おわり）

　この答えにより、上の式のように、ベクトルＢＯがベクトルａとｂとであらわせました。

　しかし、この答えでは、先に予測した公式が見えません。このようにベクトルａとｂを元にした式では、先に予測した公式を表現することができないということがこの答えによってハッキリ分かりました。

【解の変形】
　そのため、答えを表現するための基準にするベクトルを、以下の図のように、互いに垂直な単位ベクトルｘとｙに変更します。

　このベクトルｘとｙを使って、先に求めたベクトルＢＯの解を変形します。

（解の変形おわり）

　この解により、先に予測していたベクトルＤＯの長さｍが以下の図のようにあらわせました。

【第２の解】
　ベクトルａとそれに垂直なベクトルｈを使って、すなわち、単位ベクトルではないが互いに垂直なベクトルを使った解答を、
最初から述べます。

ここまでの計算は、以下の計算をするだけでも良かった。

次に、ベクトルＢＯとベクトルｂが直交する条件（内積が０）を導入して未知数ｐを求めます。

（第２の解おわり）

以上で、垂心Ｏ点の高さを与えるベクトルＤＯの計算が、比較的簡単にできました。

（計算を振り返ってどこが良かったかを考える）
　以上の計算で大事なポイントは、先に公式の解の形を予測してから正式な計算に取りかかった事でした。答えを予測してから正式な計算をしたことで、正式な計算が、「本当に予測通りの答えを導き出せるのか」という期待に背中を押されて計算できました。

　そして、式を計算していく過程で、どういう形の式に答えを導くべきかの目標がはっきりしているので、式を何に置き換えてまとめ上げるかの道に迷わず、答えを得ることができました。

　すなわち、先に予測していた事が、式を次にどのような形に変形したら良いかというガイドになりました。

　先の予測の結果で、ベクトルａに垂直な方向のベクトルＤＯの長さの公式が予測されていました。この予測のガイドに忠実に従うならば、最初から、ベクトルａに平行な単位ベクトルｘと単位ベクトルｙを基準のベクトルにしてこの問題を解くべきでした。
　もし、そうしていれば、もっと簡単にこの公式を導き出すことができました。
　そのように、先に行なった解の推測の計算は、問題を解くために、どのベクトルを基準にしたら良いかを示唆するという重要な指針を含んでいますので、問題を解くためにとても大切な役割を持っていました。

リンク：
高校数学の目次