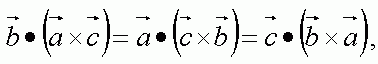ベクトルの外積（１０）

以下は、ここをクリックした先の問題の解答です。
 
【問】以下の図で三角錐ＯＡＣＢと三角錐ＯＡＣＤがある。直線ＢＤと面ＯＡＣの交点をＥとする。この場合に、比ｓ＝ＢＥ／ＢＤを求めよ。

【解答】
　この問題はベクトル方程式を立てて解くことができます。そのベクトル方程式を解くことができる実力は必要です。しかし、ベクトル方程式を解くには時間を必要とします。
　以下では、ベクトルの外積を利用して、ベクトル方程式の解を一気に計算します。

（解答おわり）

上の解は、込み入った式ですので、ベクトル方程式を解いて解を求めた場合でも、その解を、上の式のようにベクトルの内積の形で表現した方が分かりやすくて良いと思います。

（おまけ）以下の関係があります。

リンク：
高校数学の目次

ベクトル：平行平面の利用

以下は、ここをクリックした先の問題の解答です。

【問】以下の図の直線ＭＮと直線ＦＬの交点があれば、その交点Ｐを求めよ。

【解答】

（解答おわり）

　このような空間中の直線同士が交差するかどうかの判定問題は、上図のように、平行平面（面ＣＦＥと面ＤＢＡ）を利用すると分かりやすくなります。

（覚えるポイント）
　交差する２直線は同一平面上にあります。
　そのため、その２直線が平行平面と交差する点同士を結んで作ったベクトルの方向は、平行する２平面では、同じ方向になります。
　２つの空間直線が面と交差する２点を結んで作ったベクトルの方向が、２つの平行平面で異なる方向を向いたならば、その２直線は交差しません。

リンク：
高校数学の目次

ベクトルの外積で面の法線ベクトルを求める

以下は、ここをクリックした先の問題の解答です。

【問】以下の図で直線ＢＣと直線ＯＧが交差する場合のパラメータｂの値を求め、その場合の交点Ｈの座標を求めよ。




【解１】
　空間直線の交点を求める問題は、いきなり２直線のベクトル方程式を立て、それを無理やり解くのは、計算の見通しが良くないので止めましょう。
　空間直線の交点を求める問題を解く場合は、先ず、交差する２直線が乗る平面の法線ベクトルを計算しましょう。
　そして、直線をその法線ベクトルに直交させる条件を求めることで、その２直線が交点を持つ条件を確定させて計算することが大切です。
　この法線ベクトルは、平面上のベクトルの外積を計算して求めます。
　先ず、以下のようにして、面ＯＢＣの法線ベクトルＶを計算します。

　次に、この法線ベクトルＶにベクトルＧが直交する条件を求めます。法線ベクトルＶにベクトルＧが直交するなら、直線ＯＧは面ＯＢＣ上にあり、直線ＢＣと交わります。

これで、直線ＢＣと直線ＯＧが交差する場合のパラメータｂの値が求まったので、以下のようにして、この値をベクトルＧの式に代入してベクトルＧを定めます。

ベクトルＧも定まったので、以下のようにベクトル方程式を立てて交点Ｈを求めます。
　その際に、空間ベクトルをＹＺ平面に射影して、その射影を見て計算します。
（その理由）
　同一平面上にある空間直線同士の交点を求める方程式は２つで十分であり、３次元ベクトルの計算で出てくる３つの方程式では方程式が１つ余分だから、射影を利用して、その余分な方程式を減らすためです。 

 

（解１おわり）

【解２】
　面ＯＢＣを水平面であると考え、点Ｇの水平面ＯＢＣ上の高さを０にする条件を求めて、解を得ることにします。
（面ＯＢＣを水平面と考えて計算するので、計算の見通しの立て方が解１と同様です。）
　点ＧをベクトルＢＣの方向に移動しても、その点の水平面ＯＢＣに対する高さは変わりません。そのため、先ず、ベクトルＯＢからベクトルＢＣの所定倍数のクトルを引き算して、水平面ＯＢＣからの高さが同じベクトルを計算します。この計算では、ベクトルのｙ成分が０になるベクトルを残すようにします。

次に、そのベクトルから、ベクトルＯＣの所定倍数のクトルを引き算して、水平面ＯＢＣからの高さが同じベクトルを計算します。この計算では、ベクトルのｚ成分も０になるベクトルを残すようにします。

このベクトルの、水平面ＯＢＣからの高さが０になる条件は、このベクトルが０ベクトルになることです。その条件は、残ったベクトルのｘ成分が０になることであって、以下の計算で求められます。

これで、直線ＢＣと直線ＯＧが交差する場合のパラメータｂの値が求まったので、以下のようにして、この値をベクトルＧの式に代入してベクトルＧを定めます。

このあとの計算は、解１と同じ計算をします。
（解２おわり）

　ここで、賢明な読者は気付かれたと思いますが、ベクトルOＧを平面OＢＣ上に定めた時点で、もうベクトル方程式を使わないでも交点Ｈの答えが得られるようになっています。
　すなわち、この問題では、直線ＢＣはＺ＝１の平面上にありますから、ベクトルOＧのＺ座標が１になるようにベクトルOＧを９倍すれば、交点Ｈの位置ベクトルが得られます。
　見通しの良い計算をすれば、単純な問題はこのように単純に解けるようになり、計算時間を節約できる効果があります。

【解３】
　解３は、ベクトルの外積を用いない解き方ですが、以下のように解くこともできます。

　先ず、直線ＢＣと直線ＯＧが交差する場合は、ベクトルＢＣとベクトルＯＧとそして、ベクトルＯＢが同一平面上にあります。その条件を使って以下のように解くことができます。

ベクトルＢＣとベクトルＯＧとベクトルＯＢは以下の式であらわせます。

そして、ベクトルＯＢとベクトルＢＣとベクトルＯＧが同一平面上にある条件は以下の式であらわせます。

この式(4)を以下のように解きます。

これで、直線ＢＣと直線ＯＧが交差する場合のパラメータｂの値が求まったので、以下のようにして、この値をベクトルＧの式に代入してベクトルＧを定めます。

このあとの計算は、解１と同じ計算をします。
（解３おわり）

リンク：
高校数学の目次

三角形の垂心の足を結ぶ線の方向

以下はここをクリックした先の問題の解答です。

【問１】
以下の図で、三角形の頂点A及びCから対辺に下した、垂心Ｐの足DとEを結ぶ線と、頂点Bと外心Oを結ぶ線が垂直であること、すなわち、
DE⊥OB
である事を証明せよ。

【解答１】
（証明）

（証明おわり）

 【解答２】
（証明）

（証明おわり）

リンク：
高校数学の目次

軌跡（１） の解答

以下は、ここをクリックした先の問題の解答です。

【問１】
下図のように点Ａ（ａ_１，ａ_２）とＢ（ｂ_１，ｂ_２）と原点を中心とする半径ｒの円上を動く点Ｐ（ｐ_１，ｐ_２）とを頂点とする三角形の重心Ｇ（ｘ，ｙ）は、点Ｐがその円上を動くとき、どういう軌跡を動くか。その点Ｇ（ｘ，ｙ）の描く軌跡の方程式を導け。

【解答１】
先ず、動く点Ｐ（ｐ_１，ｐ_２）の円の方程式を書く

次に、重心の座標の公式を使って、重心Ｇ（ｘ，ｙ）の座標を書く。

式１に式２と式３を代入してｐ_１とｐ_２を消去したい。
そのために、式２を以下の式に変形する。

同様にして、式３を以下の式５に変形する。

この式４と式５を式１に代入してｐ_１とｐ_２を消去する。

両辺を３^２で割り算する。

この点Ｇ（ｘ，ｙ）は、中心点

を中心とする、半径

の円周上にある。
（解答おわり）

【解答２】媒介変数θを使って軌跡を計算する。
以下の式でｐ_１とｐ_２をあらわす。

 すると、以下の式でｘとｙがあらわされる。

 この２つの式を変形する。

 この２つの式のsinとcosをそれぞれ２乗して合計することで、媒介変数θを消去する。
（媒介変数θの消去方法は、この方法に限る。） 

点Ｇ（ｘ，ｙ）は、中心点

を中心とする、半径

の円周上にある。
（解答おわり）

【問２】
　次に、点Ｇがその円周上を完全に一周するかを調べよ。

【解答】
完全に一周するかどうかを調べるには、偏角をあらわすパラメータθで点Ｐの位置をあらわす。
式１を満足する点Ｐの座標Ｐ（ｐ_１，ｐ_２）は、以下の式であらわされる。
ｐ_１＝ｒ・ｃｏｓθ　（式８）
ｐ_２＝ｒ・ｓｉｎθ　（式９）
θが０から２πラジアンまで変わるとＰ点は円周を一周する。
式８と式９を式２と式３に代入する。

式１０と式１１を変形する。

式１２と式１３から、
点Ｇ（ｘ，ｙ）は、
中心点

を中心とする、半径

の円周上の偏角θの位置にあり、
θが０から２πまで変化すれば、半径（ｒ／３）の円周上を一回転する。

結局、点Ｇ（ｘ，ｙ）が円周上を一周するかどうかまで確かめなければならないので、問２を避けては通れない。
そのため、問１を解くのを省略して、問２を解いて、
点Ｇ（ｘ，ｙ）は、
中心点

を中心とする、半径

の円周上の偏角θの位置にある
という結論を得る方が効率的に全ての答えが得られる。
その円の方程式は、

とあらわせる。
（解答おわり）

リンク  
高校数学の目次

三角形の三角関数の３重積と３項和の公式

以下は、ここをクリックした先のページの問題の解答です。

【問題】

上図の、点Dを外心に持つ三角形ＡＢＣの頂点の角に関して以下の式が成り立つ事を証明せよ。

（解答の方針）
上図の三角形ＡＢＣの面積Ｓは、以下の三角関数の式であらわせます。

【解答】
先ず、正弦定理を使って、２つのsinを三角形の辺と外接円の半径Ｒであらわす。
次に、三角形の面積Ｓの公式を使う。

（解答おわり）

リンク：
高校数学の目次

三角形の三角関数の３重積と３項和の公式（２）

以下は、ここをクリックした先の問題の解答です。

【問１】
△ＡＢＣにおいて、次の等式がなりたつことを証明せよ。

【解答の心構え】
　先ず考えるべきことは、問題をもっとやさしい問題に変換できないかを考えること。
図形の問題は図を書いて考えること。
（今回は図を省略するので、図は想像して描いてください）

（解答の方針）
この問題は、式１の右辺が３つの項の掛け算だから難しい。掛け算を解消するように問題を変換する。

【解答１】
式１の右辺をＳとして、以下の式に変形する。

三角形の公式により式を変形する

これは、式１の左辺である。 
（証明おわり）

【解答２】
以下の図で考える。
先ず、三角形ABCの内接円との接点が作る三角形DEFに関して三角形の三角関数の３重積と３項和の公式を使う。

（証明おわり）

【問２】
 △ＡＢＣにおいて、次の等式がなりたつことを証明せよ。

【解答】

（証明おわり）

【問３】
三角形の外接円の半径と内接円の半径の関係
三角形ＤＥＦの内接円の半径をＲとする。
それは、三角形ＡＢＣの外接円の半径でもある。

（解答おわり）

リンク：  
高校数学の目次