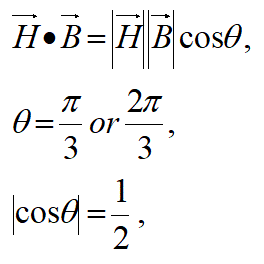円と放物線の接点を求める問題（２）

以下は、ここをクリックした先の問題の解答です。

【問１】
　以下の２つの式であらわされる円のグラフと放物線のグラフが接するｋの条件を求めよ。

【解答】
　先ずは、下図のようなグラフを描いて、問題の見通しを良くしてから問題を解きます。

図から、接点は、ｙ＝－１の点とｙ＝１の点と、それ以外にｙ座標が－１／２程度の２つの点との合計４点あると、見通しを立てます。
（それをそのまま解答にしても良い）

接点を求める問題は、微分で接点の条件を与える方程式を作ることが計算を少なくできるコツです。

そのため、以下で、微分を利用して接点の条件を与える方程式を作ります。

これにより：
この式５ｂと先の２つのグラフの式２つとの、２変数の３つの式を連立させて、ｋを求める問題に変換できました。

式５ｂから、以下の式６が得られます。

以下で、この式の２つの場合に分けて、解を求めます。

 これにより、以下の第１の解の群が得られた。

次に、式６のもう１つの場合の解を求めます。

これにより、以下の第２の解の群が得られた。

よって、式１のグラフと式２のグラフが接するようにするｋの値は、

ｋ＝±１，　－５／４
の３つです。
（解答おわり）

（補足）
　式６ｂの場合の第２の解の群は、微分を用いないでも、以下の様にして接点が２重解を持つ条件から導くことができます。
（１）＋（２）：

この２次方程式は、
ｋ＝－５／４
の場合に２重解を持ちます。
　しかし、その２重解が接点をあらわすことはあまり明確ではありません。
また、この２次方程式にこだわると、
式６ａの場合の接点の第１の解の群を見落とす恐れがあります。
　そのため、接点を求める計算では、
微分を利用した接点の条件の式５ｂを使って、式６ａと式６ｂを導き出す明確な計算によって接点を計算する方が望ましいです。 

リンク：
高校数学の目次

点Pから引いた放物線の接線の接点AとＢの中点のｘ座標は点Pと同じ

以下は、ここをクリックした先の問題の解答です。

【問１】
　以下の図のように、放物線の外側にある点Ｐから放物線に引いた２つの接線の放物線との接点を点Ａと点Ｂとする。
（１）点Ａと点Ｂの中点のｘ座標が点Ｐのｘ座標と一致することを示せ。
（２）式(1)の関係が成り立つことを示せ。


【解答】
　ｙ座標を拡大縮小した図形においても、問題の本質が変わらない。
そのため、ｙ座標を以下の図の式でＹ座標に変換して問題を解く。

放物線のグラフの関数をｆ(x) とあらわす。

この式(3)と式(4)を連立して、P点を通る直線と放物線の交点の座標（ｘ，Ｙ）を求める。
　ここで、Ｐ点を通る直線の傾きｋが放物線の交点での放物線のグラフの傾きｆ’(x) と等しくなれば、その交点は、放物線と直線との接点になる。その条件を以下の式(5)で導入して計算する。


この接線の傾きｋを与える式の中に現れた式：

の根号の中が０以上でなければ、接線の傾きｋの解が無く、接点ＡおよびＢの解が無い。この式の根号の中が０以上であることが、点Ｐから放物線に接線を引くことができる条件である。
　以上で得られた傾きｋの式に式(6)を代入して接点ＡとＢのｘ座標を求める。

　以上の式(8)と(9)とで、接点ＡとＢのｘ座標が求められた。次に、接点ＡとＢのＹ座標を求める。

次に、点Ａと点Ｂの中点Ｒの座標を求める。

式(12)により、点Ｒのｘ座標が点Ｐのｘ座標と同じであることが示された。
次に、点Ｐの真上の点Ｑまでの高さPQ＝ｇを求める。

式(17)により、式(2)の関係が成り立っている。
このため、グラフをＹ方向に拡大縮小して座標系をy座標に戻せば、式(1)が成り立っている。
（解答おわり）

リンク：
やさしい微分積分
高校数学の目次

確率の和を計算して漸化式を求める

これは、ここをクリックした先の問題の解答です。

【問１】
　袋の中に赤玉が3個、白玉が7個入っているとする。
1回の試行において、赤玉を取り出したら代わりに白玉を入れ、白玉を取り出したら代わりに赤玉を入れるとする。
Pnをn回目に赤玉を取り出す確率とする。Pnを求めよ。

【解答】
　先ず、P１を計算する。
P1=3/10,　(1)
次に、P2 を計算する。
（注意）以下の式(2)を導出する計算は、Ｐ1の値 が式(1)の値以外の場合でも成り立つ。

式(2)により、P2 を P1 であらわす式が得られた。

次に、P3 を計算する。
　以下の図で考察し、ｎ回目に玉を取り出して所定の玉を補充した後で赤玉の数が縦軸で示す数になる確率をｋ(n,i) とする。そして、ｋ(n,i) の状態の次に、n+1 回目に赤玉が取り出される確率をＤ(n,i) とする。ここで、Ｐ2は、もともとは、以下の式であらわされる。


Ｐ3の４つの項のうちｋ11の点から生じる２つの項の和を以下の式で計算する。

Ｐ3の４つの項のうちｋ12の点から生じる残り２つの項の和を以下の式で計算する。

よって、Ｐ3 を構成する４つの項の総和が、１回目の操作の結果の赤玉の数毎の確率k11と確率k12の重みの積で与えられ、以下の式で計算できる。

Ｐ4も上記のように計算した。
次に、以上の計算を種にして、全てのｎに係わる確率Ｐn の漸化式を求める。

Ｐn をあらわす式を求める。

式(10)を用いて計算したＰ2, Ｐ3 が先に求めた解と一致した。
式(10)が、求めるＰn の解である。
（解答おわり）

リンク：
高校数学の目次

6文字を円形に並べるパターンの確率（２）

これは、ここをクリックした先の問題の解答です。

【問２】
文字A,B,C,D,E,Fを円形に並べるとき
(2-1)AとBが隣り合う確率
(2-2)AとBが向かい合う確率
を求めよ。

《解答方針》
（円順列の配置パターンの確率は、円卓の席を固定して考える）
(1)円順列の円卓を固定して、その席に文字が配置される順列の数を考えて確率を求める。
(2)円卓の特定の席へ特定の文字を配置したパターンは、全員（全部の文字）を一斉に隣の席へ移動させる回転毎に異なる配置になり、結局円卓の席数倍（この問題では６倍）の数の配置がある。
(3)円卓の特定の席に特定の文字を配置した場合に、他の文字が同様に確からしく配置されるパターンを数えて配置パターンの確率を求める。

【解１】
(2-1の解答)
確率を求めるべきパターンの概要は、以下の図のようなパターンである。文字Aから見た文字Bの位置が２通りある。

下の円卓の図の上端の位置に文字Aを置いた場合に、文字Bが配置される、同様に確からしい配置は以下の図の通り５つある。

問題(2-1)の配置パターンは、これらのうち、①と⑤の２通りの配置パターンが該当する。
従って、確率=２／５
（(2-1)の解答おわり）

(2-2の解答）
　確率を求めるべきパターンの概要は、以下の図のようなパターンである。文字Aから見た文字Bの位置は１通り。

問題(2-2)の配置パターンは、先の５つの同様に確からしい配置のうち、③の１通りの配置パターンが該当する。
従って、確率=１／５
（(2-2)の解答おわり）

（補足）
　ここで、文字Aと文字Bを区別しないで黒丸●であらわした配置のパターンは、下図のようになる。

すなわち、文字Aと文字Bを区別しないであらわすと、(2-1)と(2-2)の円順列のパターンの数は、ともに１個である。
　(2-1)の配置の、文字Aの配置位置をあらゆる位置にした場合のパターンを考察する。
　先ず、文字Aと文字Bを区別しないで黒丸●であらわすと：

上図のように、６通りある。
　そのパターンの文字Aと文字Bを区別すると、以下の図の通り１２通りの配置がある。

　一方で、(2-2)の配置の、文字Aの配置位置をあらゆる位置にした場合のパターンは、
　先ず、文字Aと文字Bを区別しないで黒丸●であらわすと：

上図のように、３通りある。
　そのパターンの文字Aと文字Bを区別すると、以下の図の通り６通りの配置がある。

このように配置パターンの数に違いがあり、(2-1)の確率と(2-2)の確率に違いを生じた。
　文字Aと文字Bを区別しないで黒丸●で表わした(2-1)と(2-2)の２つのパターンは、一見すると対等に見えたが、(2-1)と(2-2)が発生する確率が異なるので、それらの黒丸●であらわした(2-1)のパターンと(2-2)のパターンは同様に確からしく生じるものではなかった。
（補足おわり）

リンク：
高校数学の目次

最後の赤玉を取り出したとき白玉が５個残る確率

これは、ここをクリックした先の問題の解答です。

【問１】
　赤玉5個と白玉10個が入っている袋の中から無作為に1個ずつ取り出す。取り出した玉は袋に戻さない。
　5個目の赤玉が取り出されたとき、袋の中に残っている白玉が5個である確率を求めよ。

【解１】
求める確率＝
(９回目までに赤４個と白５個が出る確率)(1/6)
である。

９回目までに赤４個と白５個が出る事象の連鎖には
(赤,赤,赤,赤,白,白,白,白,白)
がある。
その場合の確率＝

である。

いろいろな場合を考えると、
白５つと赤４つの順がどうであっても、
その順列の確率=

になる。

一方で、
(赤,赤,赤,赤,白,白,白,白,白)
のあらゆる並び方の数は、

である。

以上の結果を合わせると、
求める確率＝

である。
（解１おわり）

【解２】
　15個全部並べた順列の左から順に取ることにする。
右の6個が、赤、白、白、白、白、白になる順列が作られる確率を求めれば良い。
その確率は、
順列の右から順に、白、白、白、白、白、赤、・・・
になる順列が作られる確率と同じである。
順列の右から順に、白、白、白、白、白、赤、・・・
となる順列の確率＝

である。
（解２おわり）

リンク：
高校数学の目次

板の裏返しの数の確率

これは、ここをクリックした先の問題の解答です。

【問１】
　6枚のカードがあり、片面は白色が、もう片面には黒色が塗られている。これら6枚のカードを、白の面を表にしてよこ一列に並べておく。一個のさいころを投げ、nの目が出たら、左からn番目のカードをうらがえす。（n=1、2、3、、、6) このことを１回の試行とする。この試行を４回続けて行った後、黒色の面が表になったカードの枚数をxとする。
ｘ=２
となる確率を求めよ。

【解答】 
　先ず、下図のように左から右に樹形図を書いて問題を整理して、１回目の施行から４回目の施行までの確率を順次に網羅的に地道に計算する。

　この樹形図の各枝は、事象の確率の太さを持つ。この樹形図は、枝を束ねた合流点の節を持つ。合流点の節では、その合流点の事象に至る樹形図の枝の確率の和の太さになる。
　上図の樹形図に、分岐した枝の太さ（確率）と合流点の節の太さ（確率）の①から⑪を地道に計算する。
　ここで、合流点の節から分岐する２つの枝の事象の確率は、どこから合流点に至ったかにかかわらず、その合流点の節での黒面の数 ｘ にのみ依存する。
　サイコロの目が合流点の節での黒面のカード番号と同じ番号ならばそのカードが裏返されて白面になり黒面の数ｘが減る。
そう分岐する確率はｘ／６である。
　サイコロの目が合流点の節での白面のカード番号と同じ番号ならばそのカードが裏返されて黒面になり黒面の数ｘが増える。
そう分岐する確率は（６－ｘ）／６である。

　こうして枝の確率を地道に書いていくと、
上図に付記した式①から⑪の式で確率が計算できる。
上図の⑪の式が求めるｘ＝２になる確率であり、
３５／５４
である。
（解答おわり）

リンク：
高校数学の目次

ベクトルAとBに対し９０度と角度θを成すベクトル

このページは、ここをクリックした先の問題の解答をあらわす。

【問題１】
　 x軸の正の向きとのなす角が30°で、ベクトルa=(0,1,-1)に垂直な単位ベクトルを求めよ。

【解答】
　x軸の正の向きのベクトルをベクトルb=(1,0,0)とする。ベクトルｂはベクトルａに垂直である（ｘ軸はベクトルａに垂直である）。
　先ず、下図に示すように、ベクトルaに垂直で、かつ、ベクトルｂに垂直なベクトルＤを求める。ベクトルａとベクトルｂとベクトルＤとは互いに垂直である。
　
　そして、ベクトルa=(0,1,-1)に垂直で、x軸の正の向きとのなす角が30°のベクトルＨを、上式のように、ベクトルａに垂直なベクトルｂとベクトルDの合成ベクトルで表す。その式のベクトルＨはベクトルｂを含む。また、ベクトルｂはＸ軸の正の方向を向いているので、ベクトルＨとＸ軸の正の方向のベクトル（ベクトルｂ）とのなす角は９０°以下である。

　また、ベクトルｂとベクトルａに垂直なベクトルDは、以下の式のように外積の計算で求める。


　そして、ベクトルｂとベクトルHが角度θ＝３０°を成す以下の方程式を解いてベクトルHの方向を定める。


このベクトルHを単位ベクトルに変換する。

この単位ベクトルが、求める単位ベクトルである。
（解答おわり）

【問題２】
　以下の図のベクトルAに対し９０度の方向を向き、ベクトルBに対し６０度の角度、又はその逆方向（１２０度の角度）を向くベクトルHを求めよ。
（ベクトルHは、ベクトルBに対し６０度の角度を成すものでも、又は、その方向が逆向きの１２０度の角度を成すベクトルでも、どちらの方向でも良いものとする）

【解１】
　下図のように、ベクトルＢを、ベクトルＡに平行するベクトルと、ベクトルＡに垂直なベクトルＣとに分解する。
　また、ベクトルＡとベクトルＢに垂直なベクトルＤを求める。

　求めるべきベクトルＨは、上の式のように、ベクトルCとベクトルDの合成ベクトルで表す。そのベクトルＨは、ベクトルＣを含み、それ以外のベクトルの成分はベクトルＣに垂直な方向を向いているので、ベクトルＨとベクトルＢのなす角は９０°以下である。そのベクトルＨを（－１）倍したベクトル（－Ｈ）は、ベクトルＢとのなす角が９０°以上ある。

　ベクトルCは以下の式で計算する。

　ベクトルDは、以下の式の外積の計算で求める。

　そして、ベクトルBとベクトルHが角度θ＝６０°を成す方程式を解いてベクトルHを定める。


このベクトルH’が、求めるベクトルである。
（解１おわり）

《補足１》
　この種の問題は、ベクトルＢとベクトルＨのなす角度θの設定値によっては、解が無い場合がある。例えば、ベクトルＡとベクトルＢが垂直ではない場合に、ベクトルＢとＨのなす角θの値が極めて０に近い場合は、ベクトルＨがベクトルＡに垂直になることが不可能になる。
（補足１おわり）

【解２】
　ベクトルHに関して、以下の式(1)と式(2)が成り立つ。

θは６０度又は１２０度の角度である。

　解２の解き方は、先ず、ベクトルＡに垂直なベクトルを２つを求め、その２つのベクトルの和でベクトルＨをあらわして、ベクトルＨを求める、という解き方をする。

　そのために、ベクトルAに垂直な、以下の２つのベクトルｍとｎを考える。

（補足２：２つのベクトルｍとｎの別の表し方）
　ベクトルAに垂直な２つのベクトルｍとｎは、以下の様に表すこともできる。

（補足２おわり）

　この２つのベクトルｍとｎは、どちらもベクトルＡに垂直である。そのため、式(1)を満足する、ベクトルAに垂直な全てのベクトルHを、係数ｓとｔを使って以下の式であらわすことができる。

（１）ただし、ベクトルｎが、ベクトルBに対し６０度又は１２０度の角度を成す条件を満足するベクトルであったならば、求めるベクトルHを定める係数 s=0 である。

（２）そうで無ければ、ｓ≠0であり、
以下の式(3)で、未知の係数ｋを使って求めるベクトルHをあらわすことができる。
（ただし、逆方向のベクトルを表すには負の値の係数を掛け算する必要があり、大きさの異なるベクトルを表すにはその大きさの比の係数を掛け算する必要がある。）

以下のように、式3であらわすベクトルHを式2に代入して、ベクトルHを求める。

この式４の両辺を二乗する。

これで未知の係数ｋが求められたので、このｋを式3に代入して求めるベクトルHを計算する。

このベクトルHは、ベクトルAに対し９０度、ベクトルBに対し６０度又は１２０度の角度を成す。
（解２おわり）

《研究》
　解２では、ベクトルAに垂直な２つのベクトル同士は互いに垂直であるというわけではなかった。ここでは、ベクトルＡ方向の軸を持つ直交座標系の、ベクトルＡに垂直な他の軸方向の（互いに垂直な）ベクトルＶとＷ（単位ベクトル）を、（ベクトルの外積計算を利用せずに）求める方法を研究する。


このベクトルＶとＷを合成することで、ベクトルＡに垂直な全てのベクトルを作ることができる。それらの直交ベクトル系を使うと、いろいろな問題が解き易くなる。

《補足３》
　解１と解２は、解がかなり異なる形をしているが、同じ解（正負が逆ではあるが）をあらわしている。解１の方が、解答の見通しが良いので、より良い解答である。

リンク：
高校数学の目次