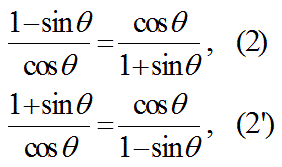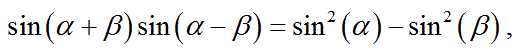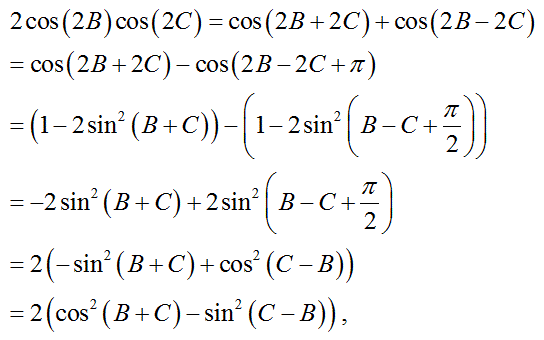以下は、ここをクリックした先の問題の解答です。
単位ベクトルA(a1,a2)と単位ベクトルB(b1,b2)について、
以下の公式を証明せよ。
 【問1】以下の公式を証明せよ。
(証明開始)
(証明おわり)
【問1】以下の公式を証明せよ。
(証明開始)
(証明おわり)
【問2】以下の公式を証明せよ
a12b22-
a22b12
=a12-b12
(証明開始)
a12b22-
a22b12
=
a12b22
+(a12b12-a12b12)
-a22b12
=a12(b22+b12)
-(a12+a22)b12
=a12-b12
=-a22+b22
(証明おわり)
これらは、公式として覚えてください。
(これらの単位ベクトルの要素をsinとcosであらわして公式をあらわすこともできます。)
式の変形の過程で以上の形の式が出てきたら、すぐ、このように式を変形できるように式の変形のコツを覚えておいてください。
リンク:
高校数学の目次
これは、ここをクリックした先のページの問題の解答です。
【問題】
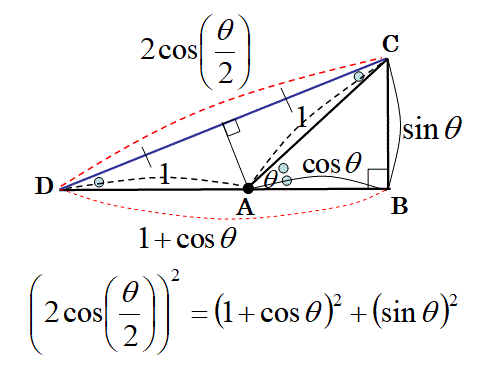
三角形の頂角を半分にした三角形に関して、
以下の式1及び2が成り立つことを証明せよ:
【式1の証明開始】
以下の三角形DBCを書く。
三角形DBCの三平方の定理の式を以下の様に変形する。
(証明おわり)
【式2の証明開始】
以下の三角形CBDを書く。
三角形CBDの三平方の定理の式を以下の様に変形する。
(証明おわり)
リンク:
高校数学の目次
これは、ここをクリックした先のページの問題の解答です。
【公式1】
分数式の分母が0になる場合を除き、
以下の式1及び1’:
が成り立つ事を証明せよ。
【証明開始】
式1又は式1’を変形する:
この計算を逆にたどることで式1が得られる。
(証明おわり)
【公式2】
分数式の分母が0になる場合を除き、
以下の式2及び2’:
が成り立つ事を証明せよ。
【証明開始】
式2又は式2’を変形する:
この計算を逆にたどることで式2が得られる。
(証明おわり)
【公式3】
分数式の分母が0になる場合を除き、
以下の式4:
及び、
が成り立つ事を証明せよ。
【証明開始】
式4又は式4’を変形する:
この計算を逆にたどることで式4が得られる。
(証明おわり)
(補足)
この式4は、以下の図からも求める事ができる。
しかし、この図から式4を導き出すよりも、先の証明の計算の方が楽に式4を導き出すことができます。
【公式4】
分数式の分母が0になる場合を除き、
以下の式5:
及び、
が成り立つ事を証明せよ。
【証明開始】
式5又は式5’を変形する:
この計算を逆にたどることで式5が得られる。
(証明おわり)
(補足)
式5は、以上の様に証明できましたが、そもそも、式5のCを((π/2)ーθ)に置き換えれば、cosC→sinθに変わり、sinC→cosθに変わり、式5は、式4の形の式に変わります。
そのように角度Cの変数の置換えをするならば、式5の形は式4の形に変換できるので、式5を考える必要がありません。
リンク:
高校数学の目次
これは、ここをクリックした先の問題の解答です。
【問1】
上図のように、XY座標軸の原点Oを頂点にする二等辺三角形OABがあり、
OA=OB
である。
辺ABの中点をMとする。
MからY軸に平行に引いた直線と、
BからX軸に平行に引いた直線の交点をNとする。
MからY軸に引いた垂線の足をQとする。
Bから辺OAに引いた垂線の足をHとする。
このとき、
三角形QMNと三角形BHAが相似であることを証明せよ。
【証明開始】
MO⊥ MB
である。
また、
MQ⊥MN
である。
よって、
△OMQ∽△BMN
よって、
よって
△QMNと△OMB
の直角をはさむ2辺の比が等しい。
また、△QMNと△OMBはいずれも直角三角形であって、1つの角度が直角で等しい。
2辺の比が等しく、その2辺の間の角度が等しいので、
△QMN∽△OMB (1)
△OMBと△BHAは、
∠OBM=∠BAH
であり、あと1つの角度が直角で等しい。
よって、2角が等しいので、
△OMB∽△BHA (2)
(1)と(2)より、
これは、ここをクリックした先のページの問題の解答です。
【公式1】
分数式の分母が0になる場合を除き、
以下の式:
が成り立つ事を証明せよ。
なお、角度CをーCに置き換えれば、式1は:
になる。
更に角度Cを(π/2)ーCに置き換えれば、式2は:
になる。
(補足)
式3の左辺の形を見たら、式3のCを((π/2)ーθ)に置き換えれば、cosC→sinθに変わり、sinC→cosθに変わり、式3は、式2の形の式に変わります。
そのように角度Cの変数の置換えをするならば、式3の形は式2の形に変換できるので、式3を考える必要がありません。
【証明開始】
式1の中間の辺を以下のように変形する。
(式1の左辺=中間の辺の証明おわり)
(式1の中間の辺=右辺の証明おわり)
(証明おわり)
(補足)
この公式1は、下図において:
MN/MQ=HC/HB
の関係がある事を示している。
それは、
△MNQ∽△HCB
であるので、
成り立っている。
(ここをクリックした先の問題を参照してください)
【公式2】
分数式の分母が0になる場合を除き、
以下の式4:
及び、
が成り立つ事を証明せよ。
【証明開始】
式4又は式4’を変形する:
この計算を逆にたどることで式4が得られる。
(証明おわり)
【公式3】
分数式の分母が0になる場合を除き、
以下の式5:
及び、
が成り立つ事を証明せよ。
【証明開始】
式5又は式5’を変形する:
この計算を逆にたどることで式5が得られる。
(証明おわり)
(補足)
式5は、以上の様に証明できましたが、そもそも、式5のCを((π/2)ーθ)に置き換えれば、cosC→sinθに変わり、sinC→cosθに変わり、式5は、式4の形の式に変わります。
そのように角度Cの変数の置換えをするならば、式5の形は式4の形に変換できるので、式5を考える必要がありません。
【公式4】
分数式の分母が0になる場合を除き、
以下の式6:
及び式7:
が成り立つ事を証明せよ。
【証明開始】
式6は、以下の計算で証明できる。
式7は、以下の計算で証明できる。
(証明おわり)
リンク:
高校数学の目次
これは、ここをクリックした先の問題の解答です。
【問1】
上図の角度の関係、すなわち、
三角形の垂心Hの周りの角度が、上図の様に、三角形の頂角と同じ角度になっていることを証明せよ。
【第1の証明開始】
先ず、下図で考える。
三角形BCEと三角形BHDは、
(1)頂角Bが同じ角度で、
(2)もう1つの頂角が
∠BEC=∠BDH=90°
であって同じなので、
(3)三角形は相似になり
△BCE∽△BHD
∴ ∠BCE=∠BHD=∠C
同様にして、
△ CAF∽△CHE
∴ ∠CAF=∠CHE=∠A
同様にして、
△ ABD∽△AHF
∴ ∠ABD=∠AHF=∠B
(証明おわり)
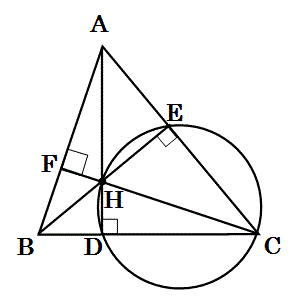
【第2の証明開始】
下図のように、三角形HCEの外接円を考える。
この外接円に内接する三角形EHCは、頂角Eが直角な三角形であるため、
辺HCは外接円の直径になる。
その外接円の辺HCの上側の円周角が90°であるので、
辺HCの下側の円周角は、
180°-90°=90°
である。
そのため、下側の円周角と等しい直角の頂角Dを持つ直角三角形HCDも
その外接円に内接する。
∴ 四辺形EHDCは三角形EHCの外接円に内接する。
拡張円周角の定理により、
三角形ABCの∠Cと同じ角度が点Hの周りの下図の位置にある。
外接円を除去して書くと以下の図になる。
同様にして、三角形ABCの他の頂角A、頂角Bも点Hの周囲の、下図の位置にある。
(証明おわり)
リンク:
中学数学の目次
高校数学の目次
【証明開始】
左辺の2倍を以下のように変形する。
(証明おわり)
【複素数平面を使った証明】
上図の様に、複素数zとwを定義する。
である。
zとwを使って問題の等式を式1に書き変える。
この式1の左辺と右辺のそれぞれを計算する。
式1の左辺は:
式1の右辺は:
式2と式3は等しい。
よって式1が成り立つ。
よって公式1が成り立つ。
(証明おわり)
(補足)
このように。複素数平面で計算できるようになれば、三角関数の加法定理や三角関数の和と積の公式を忘れても、それらの公式を使う問題を解くことができるようになります。
【公式2】
角度Bと角度Cに関して、以下の式:
又は、
又は、
が成り立つ事を証明せよ。
【証明開始】
左辺の2倍を以下のように変形する。
(証明おわり)
リンク:
高校数学の目次