このページは、ここをクリックした先の問題の解答です。
【解答】
(補足)
以上で答えが円になると分かったので、
円の式から始めて以下の計算をすることができます。
この計算で元の式が得られたので、
この式の計算を逆にして、以下の式を書き並べて
「解答」として記載することもできます。
(計算の感想)
この式になるからzは円を描くと言う「解答」をすることができます。
(多くの参考書にはそのような「解答」が書かれていると思います。)
しかし、その解答の式の変形の問題点は、無理やり円の式を導く計算をしているという点にあります。
すなわち、この計算を初めからするというのは、答えが円になると仮定して計算をしています。
もしその計算で円の式が得られなかったら計算が手詰まりになるという計算方針です。そのため、その式の変形の根拠が弱い。問題に対して解答例を覚えるだけの式である。他の問題に対しても適用できて答えが得られるという汎用性が乏しい計算方法だと思います。
汎用性の高い計算方法をこそ覚えるべきだと思います。
この計算式は、
最初に計算したように、
別の方法で 答えが円になることを知った後に、
その円の式から始めて計算して行って、初めの設問の式を得るという計算順序が自然で無理の無い計算順序だと思います。
リンク:
高校数学の目次
【解答】
(補足)
以上で答えが円になると分かったので、
円の式から始めて以下の計算をすることができます。
この式の計算を逆にして、以下の式を書き並べて
「解答」として記載することもできます。
この式になるからzは円を描くと言う「解答」をすることができます。
(多くの参考書にはそのような「解答」が書かれていると思います。)
しかし、その解答の式の変形の問題点は、無理やり円の式を導く計算をしているという点にあります。
すなわち、この計算を初めからするというのは、答えが円になると仮定して計算をしています。
もしその計算で円の式が得られなかったら計算が手詰まりになるという計算方針です。そのため、その式の変形の根拠が弱い。問題に対して解答例を覚えるだけの式である。他の問題に対しても適用できて答えが得られるという汎用性が乏しい計算方法だと思います。
汎用性の高い計算方法をこそ覚えるべきだと思います。
この計算式は、
最初に計算したように、
別の方法で 答えが円になることを知った後に、
その円の式から始めて計算して行って、初めの設問の式を得るという計算順序が自然で無理の無い計算順序だと思います。
リンク:
高校数学の目次
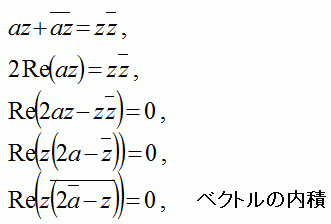



0 件のコメント:
コメントを投稿