以下は、ここをクリックした先の問題の解答です。
以下の問題は、「相似図形同士で辺の比が等しい公式」を使う問題です。
【問1】(難問)
上図のように、三角形ABCの頂角Aの二等分線の長さmに間して式1が成り立つことを証明しなさい。
(注意)
この問題は、「角の二等分線の長さの定理」であり、有名な定理ですが、その証明を見たことの無い学生にはかなりな難問です。以下の理由により、有名定理だからと言って安易に解答を見ないよう注意してください。この難問を自力で証明してから解答を見てください。
(解けるまで解答を見ない理由)
この定理よりも覚え易い定理に中線定理があります。
しかし、高校入試問題を見ると、
その中線定理を使うよう誘導している入試問題が、その誘導にもかかわらず、中線定理を使わないでも解けるようにした問題を出題しています。
その出題高校の意図を推測すると、
「単にいろいろな定理を覚えて知っている学生よりも、想像力豊かで知能が高く融通性に富んだ学生の方を合格させたい」
という意図があるように考えられます。
そのため、この「角の二等分線の長さの定理」を学ぶ目的は、
この定理を証明しようとする努力により知能を高めるホルモンが分泌されて知能を高めること、
を第1の目的にするのが良いと考えます。
そのため、この定理を自力で証明するまでは解答を見ずに、知能ホルモンの分泌を続けるのが良いと考えます。
(解答の方針)
辺の長さの積の定理は、相似図形では辺の比が同じであることに由来します。結局、辺の長さの積の定理は、ある相似図形に由来する定理です。そのため、この問題は、相似図形を探す問題です。
この問題のように、辺の長さの積の定理の問題は、
(1)図の不足を埋めて図を完成させてから、
(2)相似図形を発見して、相似図形の辺の比が等しい式を書いて
問題を解くように心がけてください。
【証明開始】
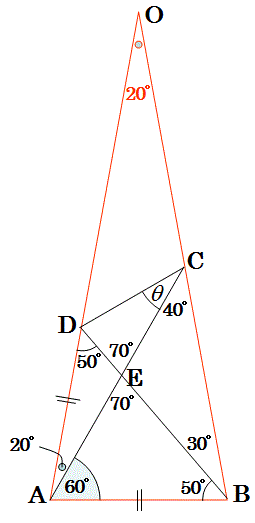
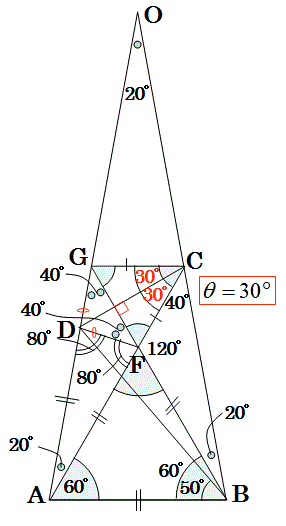
図の不足を埋めて以下の図を書きます。
この図を書いて
三角形ABEと三角形ADCが、2つの角度が等しく相似であることを発見しました。
そのため、「相似図形同士で辺の比が等しい」 公式を使い、以下の辺の比の式を書き、
その式を変形して、以下の、辺の積の式2を導き出します。
次に、以下の図のように、もう1つの相似な図形の組を発見して、
「相似図形同士で辺の比が等しい」 公式を使い、以下の辺の比の式を書きます。
こうして、相似な図形の辺の比の式を書き、
その式を変形して、上の式の、辺の積の式3を導き出します。
----(注意)---------------------
この式3は「方べきの定理」と呼ばれている有名な定理ですが、このように
「相似な図形の組を発見して辺の長さの比の式を書く」
ことに帰着されます。
そのため、「方べきの定理」を覚えるよりは、
「相似図形同士で辺の比が等しい」 公式を覚えて使う方が良いです。
----(注意おわり)---------------
この式3を式2に代入すると、求める式1が得られます。
(証明おわり)
(注意2)
この定理の式1を覚えようとしても覚えられません(何度覚えても式を忘れます)。
そのため、この定理の式を覚えるには、この定理の要になる、上図の、三角形の外接円と、円周角の定理によって角度が等しい相似な図形のイメージを覚えて下さい。そうすれば、その図のイメージがヒントになって、相似の図形の辺の比例の式(定理の式と同等)が速やかに導き出せるようになります。
この定理と、それ以外の類似した定理の全ては、以下の3つの図の相似な三角形の組み合わせのイメージを覚えるだけで、それらのイメージから得られる情報を使って、全てを求めることができます。
そのため、それらの定理の式を実践の場で使える応用力をつけるには、それらのイメージを覚え、その図のイメージの相似な図形の辺の比例の式(定理の式と同等)を図から導き出してください。それらの相似な図形の辺の比例の式は、定理の式が変形された定理の式と同等な式なので、それらの式を使えば、定理の式を使うのと同じく問題を解くことができます。
【研究問題】
公式が覚えられないという真実も知って、覚えられない公式を速やかに導き出す方法も知った学生は、もう高校1年生と完全に同等(以上)の数学センスを持つ学生と思います。
そこまで数学が分かったならば、当初の定理で得た式は、実はもっと先にまで変形できるという事も、研究して知っても良いと思います。
以下で、当初の定理の式を導くところから始めて、式をもっと先にまで変形してみます。
上の図の式を以下の式に変形します。
ここで、以下の関係が成り立ちます。
この関係を式1に代入する。
(研究問題の解答おわり)
この式2によって、角の二等分線の長さmを、三角形の辺a,b,cで求める式が得られました。
(この式2は覚える事はとても困難な式ですが、以上の手順でいつでも導き出すことができます。それは、定理の式を覚えているのと同じ事だと思います。)
リンク:
中学数学の目次
以下の問題は、「相似図形同士で辺の比が等しい公式」を使う問題です。
【問1】(難問)
(注意)
この問題は、「角の二等分線の長さの定理」であり、有名な定理ですが、その証明を見たことの無い学生にはかなりな難問です。以下の理由により、有名定理だからと言って安易に解答を見ないよう注意してください。この難問を自力で証明してから解答を見てください。
(解けるまで解答を見ない理由)
この定理よりも覚え易い定理に中線定理があります。
しかし、高校入試問題を見ると、
その中線定理を使うよう誘導している入試問題が、その誘導にもかかわらず、中線定理を使わないでも解けるようにした問題を出題しています。
その出題高校の意図を推測すると、
「単にいろいろな定理を覚えて知っている学生よりも、想像力豊かで知能が高く融通性に富んだ学生の方を合格させたい」
という意図があるように考えられます。
そのため、この「角の二等分線の長さの定理」を学ぶ目的は、
この定理を証明しようとする努力により知能を高めるホルモンが分泌されて知能を高めること、
を第1の目的にするのが良いと考えます。
そのため、この定理を自力で証明するまでは解答を見ずに、知能ホルモンの分泌を続けるのが良いと考えます。
(解答の方針)
辺の長さの積の定理は、相似図形では辺の比が同じであることに由来します。結局、辺の長さの積の定理は、ある相似図形に由来する定理です。そのため、この問題は、相似図形を探す問題です。
この問題のように、辺の長さの積の定理の問題は、
(1)図の不足を埋めて図を完成させてから、
(2)相似図形を発見して、相似図形の辺の比が等しい式を書いて
問題を解くように心がけてください。
【証明開始】
図の不足を埋めて以下の図を書きます。
三角形ABEと三角形ADCが、2つの角度が等しく相似であることを発見しました。
そのため、「相似図形同士で辺の比が等しい」 公式を使い、以下の辺の比の式を書き、
その式を変形して、以下の、辺の積の式2を導き出します。
次に、以下の図のように、もう1つの相似な図形の組を発見して、
「相似図形同士で辺の比が等しい」 公式を使い、以下の辺の比の式を書きます。
こうして、相似な図形の辺の比の式を書き、
その式を変形して、上の式の、辺の積の式3を導き出します。
----(注意)---------------------
この式3は「方べきの定理」と呼ばれている有名な定理ですが、このように
「相似な図形の組を発見して辺の長さの比の式を書く」
ことに帰着されます。
そのため、「方べきの定理」を覚えるよりは、
「相似図形同士で辺の比が等しい」 公式を覚えて使う方が良いです。
----(注意おわり)---------------
この式3を式2に代入すると、求める式1が得られます。
(証明おわり)
(注意2)
この定理の式1を覚えようとしても覚えられません(何度覚えても式を忘れます)。
そのため、この定理の式を覚えるには、この定理の要になる、上図の、三角形の外接円と、円周角の定理によって角度が等しい相似な図形のイメージを覚えて下さい。そうすれば、その図のイメージがヒントになって、相似の図形の辺の比例の式(定理の式と同等)が速やかに導き出せるようになります。
この定理と、それ以外の類似した定理の全ては、以下の3つの図の相似な三角形の組み合わせのイメージを覚えるだけで、それらのイメージから得られる情報を使って、全てを求めることができます。
そのため、それらの定理の式を実践の場で使える応用力をつけるには、それらのイメージを覚え、その図のイメージの相似な図形の辺の比例の式(定理の式と同等)を図から導き出してください。それらの相似な図形の辺の比例の式は、定理の式が変形された定理の式と同等な式なので、それらの式を使えば、定理の式を使うのと同じく問題を解くことができます。
【研究問題】
公式が覚えられないという真実も知って、覚えられない公式を速やかに導き出す方法も知った学生は、もう高校1年生と完全に同等(以上)の数学センスを持つ学生と思います。
そこまで数学が分かったならば、当初の定理で得た式は、実はもっと先にまで変形できるという事も、研究して知っても良いと思います。
以下で、当初の定理の式を導くところから始めて、式をもっと先にまで変形してみます。
ここで、以下の関係が成り立ちます。
この関係を式1に代入する。
(研究問題の解答おわり)
この式2によって、角の二等分線の長さmを、三角形の辺a,b,cで求める式が得られました。
(この式2は覚える事はとても困難な式ですが、以上の手順でいつでも導き出すことができます。それは、定理の式を覚えているのと同じ事だと思います。)
リンク:
中学数学の目次