ラングレーの難問

以下は、ここをクリックした先の問題の解答です。

以下の問題の解答は、通算１４時間以上、この問題を解こうと試みた学生、又は自力で解答を得た学生が見てください。
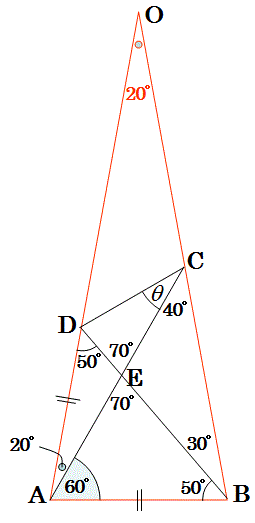
【問】（超難問）

上図の四角形ＡＢＣＤにおいて、角ＡＣＤ＝θを求めなさい。

（注意）
　図形問題では、
先ず、補助線を引いて足りない図形は埋め、
同じ角度に印を付けつつ、
図形を対称な形に完成させてから問題を解くように心がけてください。
　特に、この図形問題では、対称性が特に高い正三角形を含む対称な形の図形を完成させてから問題を解くようにしてください。

【解答】
　この問題は、以下の順に、図形をほぼ対称な形になるように補助線を引いていきます。
（１）先ず、分かっている角度を埋めます。

（２）
∠ＯＡＢ＝∠ＯＢＡ＝８０°に注目して、以下の二等辺三角形ＯＡＢを書きます。

（３）
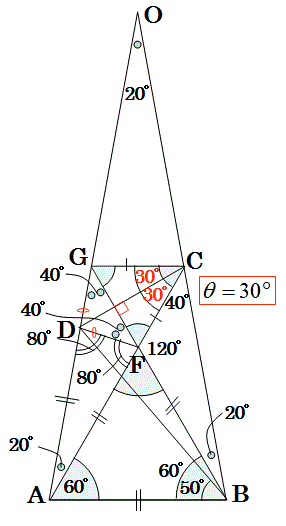
この図形に補助線を引いて、対称な形にし、しかも正三角形を加えます。

（４）
ＡＤ＝ＡＦ
から、三角形ＡＤＦは二等辺三角形だとわかります。

（５）
∠ＡＦＤ＝８０°
なので、
∠ＤＦＧが計算できます。

（６）
三角形ＤＦＧが二等辺三角形だと分かりましたので、
線分ＣＤは線分ＧＦの垂直二等分線だと分かります。

よって、 
∠ＡＣＤ＝θ＝３０°
です。
（解答おわり）

リンク：
中学数学の目次