180度の５分の１の頂角の二等辺三角形の辺の長さ

以下は、ここをクリックした先の問題の解答です。

【問１】

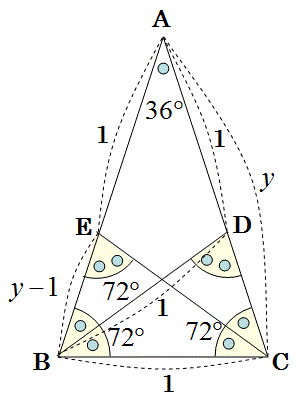
上の図のように、１８０度の５分の１の３６度の頂角Ａを持つ二等辺三角形ＡＢＣがある。
この二等辺三角形の辺の長さｙを、補助線ＣＥとＢＤを利用して解け。
ただし、線分ＢＤは∠Ｂの二等分線であり、線分ＣＥは∠Ｃの二等分線である。

【解答】
　上の足りない図（角度の記述）を埋めて下図を得る。

三角形ＢＣＤは二等辺三角形であり、
１＝ＢＣ＝ＢＤ
である。
 三角形ＤＡＢは二等辺三角形であり、
１＝ＤＢ＝ＤＡ
である。
その記述も上図に加えた。

上図から、
⊿ＣＢＥ∽⊿ＡＢＣなので、
三角形の辺の間に以下の関係が成り立つ。
ＥＢ÷ＢＣ＝ＢＣ÷ＣＡ
この関係を変数ｙであらわす方程式１を作る。

方程式１を解いて式２を得、
不適な解を除去して解の式３を得た。
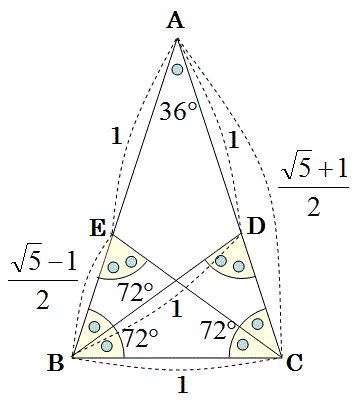
よって、二等辺三角形ＡＢＣの辺の長さは、
下図の通りである。

（解答おわり）

（補足）
頂角３６°の二等辺三角形の斜辺：底辺の比は、

となります。
そのため、以下の式４が成り立つことになります。

この式４が成り立つことは、実際に計算すれば、そうだと分かります。
（チョット便利なこと）
　この式４を覚えておくと、この式４のどれかの項の逆数を求めるとき、計算しないで答えを出せるのでチョット便利だと思います。

リンク：
中学数学の目次