これは、ここをクリックした先の問題の解答です。
【問1】(難問)
さいころをn個同時に投げるとき、出た目の数の和がn+3になる確率を求めよ。
(2006年 京都大学)
【解答】
先ず、問題の一部で良いので、とにかく図に書きます。
樹形図を書いて整理する。
(2と3の目が出る場合)
このうち(2)の、2と3の目が出る場合は:
(n-2)個のさいころの目が1であり、
2個のさいころの目が1ではない(2か3の目)場合である。
この場合の確率の計算は以下の様に計算する。
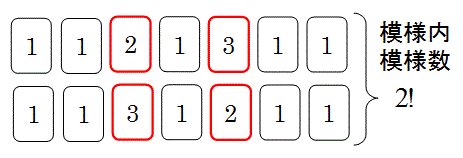
先ず上図の様に、2か3の目が出る2つのさいころの場所の模様の数を計算します。
次に、上図の様にその模様の内部を2にするか3にするかの模様内模様の数を計算します。
これら2つの組み合わせの数の積が場合(2)における全模様の数です。
こうして、解答のめどが立ったら、もう一度問題に注意します。
この問題は、さいころの数nが定まっていない問題なので、nの数によっては、上の場合が生じ得ないこともあるので、注意します。
(A) n≧3の場合の確率:

(式のチェック)
このように変数nの式を求めたら、この式に間違いが無いかをチェックする。
n=3の場合を代入すると、
3×4×5/64=10/63 になる。
(n=3の場合は、
2と3が出る組み合わせが3×2=6通り、
4が出る組み合わせが3通りあり、
全て1になる組み合わせが1通りあり、
合計10通りの組み合わせがあるので、
この答えは正しいことが確認できた。)
(B)n=2の場合の確率:
この計算でn=2の場合の答えが、(A)で得た、n≧3で得た計算式であらわせるかどうかの知的好奇心によるチェックをすることを忘れないようにしましょう。
計算の結果、あらわせることがわかりました。
(C)n=1の場合の確率:
この計算でもn=1の場合の答えが、(A)で得た、n≧3で得た計算式であらわせるかどうかの知的好奇心によるチェックをすることを忘れないようにしましょう。
計算の結果、これもあらわせることがわかりました。
よって、(A)の場合の式がn≧1の全ての場合の答えをあらわす。
(解答おわり)
リンク:
高校数学の目次
【問1】(難問)
さいころをn個同時に投げるとき、出た目の数の和がn+3になる確率を求めよ。
(2006年 京都大学)
【解答】
先ず、問題の一部で良いので、とにかく図に書きます。
(2と3の目が出る場合)
このうち(2)の、2と3の目が出る場合は:
(n-2)個のさいころの目が1であり、
2個のさいころの目が1ではない(2か3の目)場合である。
この場合の確率の計算は以下の様に計算する。
これら2つの組み合わせの数の積が場合(2)における全模様の数です。
こうして、解答のめどが立ったら、もう一度問題に注意します。
この問題は、さいころの数nが定まっていない問題なので、nの数によっては、上の場合が生じ得ないこともあるので、注意します。
(A) n≧3の場合の確率:

(式のチェック)
このように変数nの式を求めたら、この式に間違いが無いかをチェックする。
n=3の場合を代入すると、
3×4×5/64=10/63 になる。
(n=3の場合は、
2と3が出る組み合わせが3×2=6通り、
4が出る組み合わせが3通りあり、
全て1になる組み合わせが1通りあり、
合計10通りの組み合わせがあるので、
この答えは正しいことが確認できた。)
(B)n=2の場合の確率:
この計算でn=2の場合の答えが、(A)で得た、n≧3で得た計算式であらわせるかどうかの知的好奇心によるチェックをすることを忘れないようにしましょう。
計算の結果、あらわせることがわかりました。
(C)n=1の場合の確率:
この計算でもn=1の場合の答えが、(A)で得た、n≧3で得た計算式であらわせるかどうかの知的好奇心によるチェックをすることを忘れないようにしましょう。
計算の結果、これもあらわせることがわかりました。
よって、(A)の場合の式がn≧1の全ての場合の答えをあらわす。
(解答おわり)
リンク:
高校数学の目次







0 件のコメント:
コメントを投稿