これは、ここをクリックした先のページの問題の解答です。
【問1】
上の三角形において、上のベクトルの内積の式が成り立つことを証明せよ。
【解答】
先ず、ベクトルbとcを、外心から引いたベクトルAとBとCであらわす。
この式の最後の項の、ベクトルBとCの内積を、ベクトル(B+C)であらわす。
これを使って、上の式を変形する。
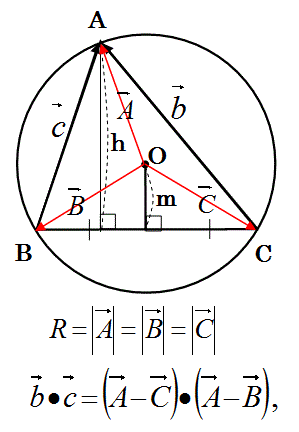
このベクトル(B+C)は、以下の図の様に単位ベクトルyに平行である。
そのため、ベクトルbとcの内積の上の式は、以下の様に変形できる。
(証明おわり)
ベクトルの切替の公式を適用した解答を以下に示す。
【問1】
上の三角形において、上のベクトルの内積の式が成り立つことを証明せよ。
【解答1】
先ず、ベクトルbとcを、外心から引いたベクトルAとBとCであらわす。
この式を、大きさRが等しいベクトルAとBとCの内積であらわし、式を変換する。
ここでベクトル(B+C)は、上図の辺BCに垂直であり、長さが2mである。
(証明おわり)
【解答2】
ここをクリックした先に、別の解答方法がある。
リンク:
高校数学の目次
【問1】
【解答】
先ず、ベクトルbとcを、外心から引いたベクトルAとBとCであらわす。
この式の最後の項の、ベクトルBとCの内積を、ベクトル(B+C)であらわす。
これを使って、上の式を変形する。
このベクトル(B+C)は、以下の図の様に単位ベクトルyに平行である。
そのため、ベクトルbとcの内積の上の式は、以下の様に変形できる。
ベクトルの切替の公式を適用した解答を以下に示す。
【問1】
上の三角形において、上のベクトルの内積の式が成り立つことを証明せよ。
【解答1】
先ず、ベクトルbとcを、外心から引いたベクトルAとBとCであらわす。
この式を、大きさRが等しいベクトルAとBとCの内積であらわし、式を変換する。
ここでベクトル(B+C)は、上図の辺BCに垂直であり、長さが2mである。
(証明おわり)
【解答2】
ここをクリックした先に、別の解答方法がある。
リンク:
高校数学の目次


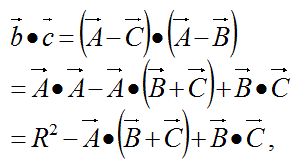





0 件のコメント:
コメントを投稿