勉強しよう数学解答集: 全部の場合を数え上げる確率の入試問題１の解答

これは、ここをクリックした先の問題の解答です。

【問１】（難問）
箱の中に、１から９までの番号を１つずつ書いた９枚のカードが入っている。
ただし、異なるカードには異なる番号が書かれているものとする。
この箱から２枚のカードを同時に選び、小さいほうの数をＸとする。
これらのカードを箱に戻して、
再び２枚のカードを同時に選び、小さいほうの数をＹとする。
Ｘ＝Ｙである確率を求めよ。
(2011年　京都大)

【解答１】
先ず、問題の一部で良いので、とにかく図に書きます。

（１）２つのカード（第１のカード組）を選ぶ全ての場合の数が上図で計算できる。

（２）次に、問題の条件の１つを満足する第１のカード組の具体的な場合を考える。
（２－１）先ず、Ｘ＝８の場合を考える。

（２－２）次に、具体的に、もう１つの条件を満足する第１のカード組を考える。
Ｘ＝１の場合を考える。

（２－３）具体的に、第１のカード組と、第２のカード組同士の、問題の条件を満たす組み合わせを考える。
Ｘ＝１の第１のカード組とＹ＝１の第２のカード組を考える。

問題の条件における、
Ｘ＝Ｙ＝１の条件を満足するカード組の全ての組み合わせの数は、
８×８＝６４通りである。

（３）問題の全貌を表す以下の図の基本樹形図を、自分の頭の中で想像して問題を整理する。
（この図は大きな図で、とても書ききれないのでこの基本樹形図は自分の頭の中で想像するだけにして紙には書かない。）

　この基本樹形図から、第１のカード組の１つの事象毎の確率がわかる。
　それを２回繰り返した、第１のカード組の事象と第２のカード組の事象との組み合わせの１つ毎の確率は、第１のカード組の１つの事象の確率の２乗ということがわかる。

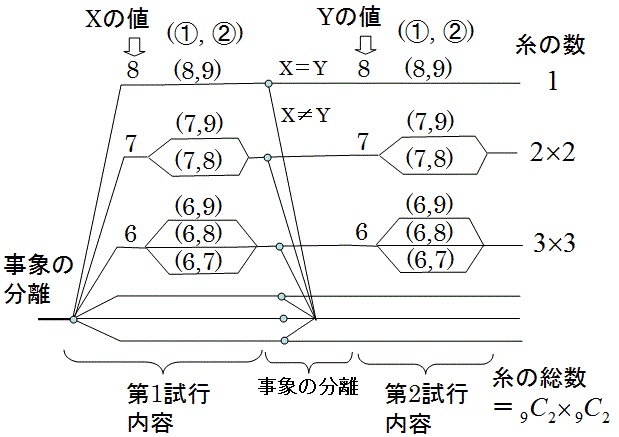
（４）上図の樹形図を整理した以下の樹形図を頭の中で想像する。

この樹形図では、左側で第１のイベントの事象毎に枝を分岐させ、その枝を一部で束ね、その後に右側の第２のイベントの事象毎に枝を分岐させている。

　この基本樹形図のうち、以下の部分樹形図なら紙に書くことができるので、それを紙に書いて状況を整理する。

このように、部分樹形図の枝を構成する事象の連鎖の糸の本数（組合せの数）がわかる。

（５）全てのＸ＝Ｙの第１のカード組と第２のカード組の組み合わせの数（糸の本数）について成り立つ法則を推測する。

問題の条件を満足する組み合わせの数（糸の本数）は、
（９－Ｘ）^２通りである。
組合せの数は、カード組の選択を２回繰り返した場合に細分化された基本樹形図の糸（末端の枝でもある）の本数である。

その糸の本数に、第１のカード組と第２のカード組の１つの組み合わせが生じる確率を掛け算することで、
１つの値のＸ＝Ｙを満足するカード組の組み合わせの群の確率が求められる。

次に、求めるべき確率ｋを計算する式を作る。