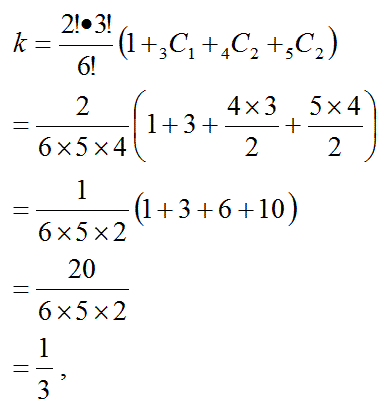勉強しよう数学解答集: 12月 2016

2016年12月31日土曜日

最初に戻る確率の入試問題８の解答

これは、ここをクリックした先の問題の解答です。

【問１】（難問）
「一つのサイコロを振り，出た目が4以下ならばAに1点を与え，5以上ならばBに1点を与える」
という試行を繰り返す。
(1)AとBの得点差が2になったところでやめて得点の多い方を勝ちとする．n回以下の試行でAが勝つ確率ｐ_ｎを求めよ。
（1992 一橋大）

【解答】
先ず、以下の樹形図を書いて問題を整理する。

図と確率を整理して書く。

最初の状態が繰り返しあらわれることがわかりました。

この最初の状態が問題の鍵です。
最初の状態が繰り返される確率を使ってＡが勝つ確率を計算する。

ｎ＝２回目からｎ＝２ｋ＋２回目までにＡが勝つ確率は上の式で計算できる。
これを、一般化した式で書く。

この式は、ｋ＝０の場合も正しい答えを与える。
よって、この問題の答えは、以下のようになります。

ｎが奇数回の場合は、ｎ－１回＝偶数回目に最初の状態に戻ってからの１回目であるのでＡもＢも勝っていない状況にあるか、
あるいは、ｎ－１回目か、それ以前にＡが勝っている状態にあることが可能である。

（解答おわり）

リンク：
高校数学の目次

2016年12月30日金曜日

自然数の数の入試問題７の解答

これは、ここをクリックした先の問題の解答です。

【問１】
３桁の自然数のうち、５の数字を１回以上用いている奇数の数を求めよ。
（神奈川大・経）

【解答１】
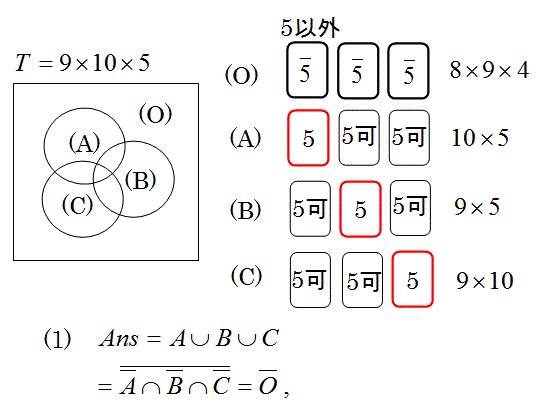
先ず、問題の一部で良いので、とにかく図に書きます。
事象Tは３けたの奇数の数をあらわします。
３桁目が１〜９の９個。
２桁目が０〜９の１０個。
１桁目が奇数の数の５個。
合わせて：
T＝９×１０×５個です。

Ｏの余事象を計算する：

（解答おわり）

【解答２】
　大学に入って「組み合わせ数学」の授業を受けると、以下のきれいな解き方を教わります。
　努力して大学に入って、ぜひ「組み合わせ数学」の授業も受けてください。

（解答はじめ）
先ず、以下の関係式が成り立ちます。

この関係式を計算する。

（解答おわり）

【解答３】
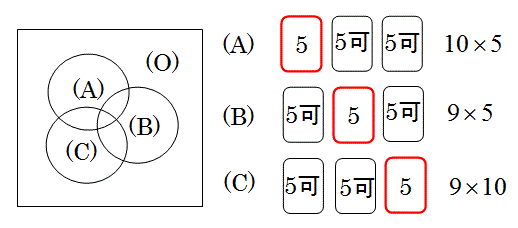
　以下の解答では、過不足無く数え上げることが大切です。しかし、その足し合わせる領域を間違え易いという問題があります。
　その間違いを防ぐために、場合の数を数える式を書く都度に左の図を塗り込んでいき、全部の領域を過不足無く塗りつぶす式を作って下さい。

（解答おわり）

リンク：
高校数学の目次

2016年12月29日木曜日

模様数と確率分の積を考える確率の入試問題５の解答

これは、ここをクリックした先の問題の解答です。

【問１】
　赤玉３個と白玉７個が入っている袋から無作為に１個を取り出し、色を確認してから袋に戻す操作を３０回繰り返すとき、赤玉を何回取り出す確率が最も大きいか答えよ。
（2013年　武庫川女子大）

【解答】
　先ず、樹形図の糸＝事象の連鎖を以下のように書いて問題を整理する。

樹形図の糸と事象の連鎖を以下の図のように対応付けて考える。

これで、事象の連鎖の確率＝樹形図の糸の太さがわかる。

それと、問題の一部で良いので、とにかく図に書きます。

３０回の試行の事象の連鎖において、赤の数が同じ事象の連鎖＝樹形図の糸は、同じ確率＝樹形図の同じ太さの糸である。
　赤の数毎に事象の連鎖を１まとめに分類することは、（赤の数による）同じ確率の事象の連鎖を集める（樹形図における同じ太さの糸を集めた枝を作る）ことに相当する。
　これに従って、同じ太さの糸を集めた枝を持つ以下の樹形図を書いて問題を整理する。

赤玉ｎ個を取り出す場合の確率を計算する：

次に、答えと思われる取り出し個数３０×（０．３）＝９個の前後の個数を比較する。

引き算よりも割り算の比較が簡単そうなので割り算して比較する。

赤９個の確率が一番大きい。
次に、一般的にこれが成り立つことを証明する計算を行う。

ｎが８個以下の場合は、ｎ＋１個取り出す方がｎ個取り出すよりも確率が高い。
ｎが９個以上の場合は、ｎ＋１個取り出す方がｎ個取り出すよりも確率が低い。
よって、９個取り出す確率が最も高い。
（解答おわり）

リンク：
高校数学の目次

2016年12月28日水曜日

模様内模様を考える確率の入試問題６の解答

これは、ここをクリックした先の問題の解答です。

【問１】（難問）
さいころをｎ個同時に投げるとき、出た目の数の和がｎ＋３になる確率を求めよ。
（2006年　京都大学）

【解答】
先ず、問題の一部で良いので、とにかく図に書きます。

樹形図を書いて整理する。

（２と３の目が出る場合）
　このうち（２）の、２と３の目が出る場合は：
（ｎ－２）個のさいころの目が１であり、
２個のさいころの目が１ではない（２か３の目）場合である。

この場合の確率の計算は以下の様に計算する。

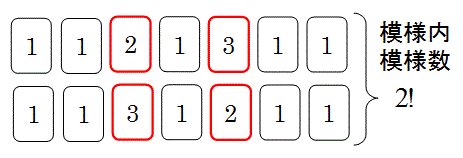
先ず上図の様に、２か３の目が出る２つのさいころの場所の模様の数を計算します。

次に、上図の様にその模様の内部を２にするか３にするかの模様内模様の数を計算します。
　これら２つの組み合わせの数の積が場合（２）における全模様の数です。

　こうして、解答のめどが立ったら、もう一度問題に注意します。
この問題は、さいころの数ｎが定まっていない問題なので、ｎの数によっては、上の場合が生じ得ないこともあるので、注意します。

（Ａ）ｎ≧３の場合の確率：

（式のチェック）
このように変数ｎの式を求めたら、この式に間違いが無いかをチェックする。
ｎ＝３の場合を代入すると、
３×４×５／６^４＝１０／６^３になる。
（ｎ＝３の場合は、
２と３が出る組み合わせが３×２＝６通り、
４が出る組み合わせが３通りあり、
全て１になる組み合わせが１通りあり、
合計１０通りの組み合わせがあるので、
この答えは正しいことが確認できた。）

（Ｂ）ｎ＝２の場合の確率：

この計算でｎ＝２の場合の答えが、（Ａ）で得た、ｎ≧３で得た計算式であらわせるかどうかの知的好奇心によるチェックをすることを忘れないようにしましょう。
計算の結果、あらわせることがわかりました。

（Ｃ）ｎ＝１の場合の確率：

この計算でもｎ＝１の場合の答えが、（Ａ）で得た、ｎ≧３で得た計算式であらわせるかどうかの知的好奇心によるチェックをすることを忘れないようにしましょう。
計算の結果、これもあらわせることがわかりました。

よって、（Ａ）の場合の式がｎ≧１の全ての場合の答えをあらわす。
（解答おわり）

リンク：
高校数学の目次

2016年12月27日火曜日

これは、ここをクリックした先の問題の解答です。

【問１】
中の見えない袋の中に同じ大きさの白球３個、赤球２個、黒球１個が入っている。
この袋から１球ずつ球を取り出し、黒球を取り出したときに袋から球を取り出すことをやめる。
ただし、取り出した球はもとに戻さない。
この試行を行なうとき、以下の問いに答えよ。
(1)取り出した球の中に、赤球がちょうど２個含まれる確率を求めよ。
（2006年　大阪府立大）

【基本樹形図による解答１】
先ず、問題の一部で良いので、とにかく図に書きます。

配置図を具体的図に書きます。

以下の基本樹形図を書いて問題を整理します。

この樹形図は、以下の図のように、（赤球2つ模様数）の枝を分岐させた後で節に合流させ、その節から再び（赤模様中配置順数）の枝を分岐させた形で樹形図を書いています。

上図のように、樹形図の最小構成要素の糸の形を、根から展開し、節に収束させ、再び節から展開する、波状の形を持たせた樹形図です。

糸の太さ（確率）は、以下の事例で示すように、赤球の数と白球の数と黒球の数の合計数（以下の事例では４球）によって定まる。

すなわち、取り出す球の数が同じ場合は、出る球の順番がどうであれ、１本の事象の連鎖の糸の太さ（確率）が同じになる。
その理由は：
（そのイベントで、１つの事象が起きる確率）
＝１／（そのイベントで選べる球の数）
だからであり、
（イベントの連鎖で１つの事象の連鎖（糸）が起こる確率）
＝各イベントで１つの事象が起きる確率の積
だからです。

　この最細枝の確率に赤模様中配置順数と白模様中配置順数を掛け算すれば枝の太さが計算できる。
よって、それらの総和の、求める確率ｋは以下の式で計算できる。

（解答おわり）

【解答２】
（解答２の考え方）
　解答１で用いた基本樹形図は枝の末端の太さが揃っていないので不便です。
　解答１の球の並びの図の（１－１）では、３回目の球の取り出しで黒球を取り出したので、それ以上袋から球を取り出すことを止めます。
　しかし、（１－２）の場合では、３回では球の取り出しが終わっていないので、（１－１）が（１－２）の場合よりもどれだけ起こり得るのか、起こり得ないのか、比較するにはどうしたら良いか。
　これを改善するために、黒球が出た後でも、下図の様に球を取り出す空試行を行なう事を想定します。

　空試行を行なうことを反映して枝を再分割して、枝の末端の太さを揃えた以下の樹形図を作ることができます。

この樹形図の意味は以下の様に考えます。
上の樹形図のポイントを下図のように書き出します。

　解答１の（１－２）の場合の確率は、袋から３個の球を取り出して（１－２）の途中の状態に至る確率に、残りの３個の球のうち（黒）を取り出す１／３の確率を掛け算した値が最終的な（１－２）の確率です。
　ここで掛け算する１／３の確率は、袋から３球を取り出した後で残りの３個の球を選べる３つのバラエティのうちの１つを選んで（黒）を取り出す確率です。

　別の視点から考えると、
　解答１の（１－１）の後では、球が袋の中に３個の球が残っているので、その残りの白球の取り出しのバラエティが３！組あります。
　それに対し解答１の（１－２）の後では、（１－２）で４球を取り出すことでバラエティの一部が使われて、袋の中の球が２個に減ったので、その残りの白球の取り出しのバラエティが２！組に減りました。
　解答１の（１－１）、（１－２）それぞれの場合の数に、残り白球が選べるバラエティを掛け算した上で、全部の球６個を取り出すあらゆる場合の数の６！で割り算して求めた値が（１－１）と（１－２）それぞれの確率であるとも言えます。

　例えば、（１－１）の場合の確率を、
（１－１）の場合の数を、球を３個取り出す球の選択の自由度の数（＝６×５×４）で割り算して求めた値は、
（１－１）の場合の確率を、（１－１）の場合の数に３！のバラエティを掛け算した上で、全部の球６個を取り出すあらゆる場合の数の６！で割り算して求めた値と同じです。

どちらの計算方法で計算しても確率の値が変わらないのです。

　この計算方法は、確率の値が変わらない計算方法であって、玉を取り出す回数が変わっても通用する確率の計算方法です。

　結局、（１－１）でも（１－２）でも、（１－３）も、（１－４）も、残りの球も空試行で取り出す全ての場合の数を計算した上で、
それらの場合の数を、全部の球を取り出す場合の数６！で割り算した値が、それぞれの場合の確率を表しています。
　このように考えて枝を再分割した樹形図が解答２の樹形図です。

　解答２の樹形図を使って、それらの総和の、求める確率ｋは以下の式で計算できる。

（解答おわり）

【解答３】
　以下の様にして、空試行のテクニックも使って、場合の数をことごとく数え上げて確率を計算することもできます。

黒玉を取り出す前に赤玉を２個取り出す場合の樹形図。
（ただし、黒玉を取り出した後も玉を取り出す空試行もあらわす。）
この樹形図で、Ａは、残りのどの玉を取り出しても良い場合をあらわします。

黒玉を取り出す前に赤玉を２個取り出す場合の数は：

よって、黒玉を取り出す前に赤玉が２個取り出される確率は：

（解答おわり）

リンク：
高校数学の目次

空試行を考える確率の入試問題３の解答

これは、ここをクリックした先の問題の解答です。

【問１】
１個のサイコロを振るという試行を繰り返す。
奇数の目が連続して３回出るか偶数の目が通算して４回出たら試行を終了するものとする。
(1)この試行が６回以下で終了する確率を求めよ。
(2)この試行がちょうど７回で終了する確率を求めよ。
（2003年　上武大）

【解答】
(1)の解答：
先ず、以下のように、事象の連鎖を表現します。
奇数を１とし、偶数を０として、１回目から６回目までの事象の連鎖の種々の場合を以下のように表現します。
終了しない場合：
(1,0,1,0,1,0)
(1,0,1,1,0,1)

（終了する場合Ａ）奇数の目が連続して３回出る
(0,1,0,1,1,1)
（終了する場合Ｂ）偶数の目が通算して４回出る
(0,1,0,1,0,0)

（問題の注目点）
（場合Ａ）奇数の目が連続して３回出る。
（場合Ｂ）偶数の目が通算して４回出る。
この２つの場合の、場合Ａや場合Ｂが生じて終了条件が満足された後でも、空試行を続けることにして、どの場合でも試行を６回まで行なうようにしてみる。そうしても、その６回の試行のどの連鎖であっても、場合Ａと場合Ｂが同時に生じる事が無い、という問題の特徴があります。
　そのため、空試行を含む６回の試行においては、場合Ａと場合Ｂとは、互いに独立して生じる事象の連鎖と考える事ができ、１つの場合毎に事象の連鎖の確率を計算して加え合わせる事ができます。

先ず、場合Ｂの確率が、場合Ａの確率よりも求め易いので、先に計算します。

（場合Ｂの計算）
　この場合Ｂの確率は、以下の樹形図を書いて計算することができる。

（補足）
　この樹形図は、枝の分岐の割合が、太さが単純に２分の１なので、各枝の太さが簡単に計算できました。しかし、枝の分岐の割合が複雑な場合は、この図で各枝の太さの計算を繰り返すのが煩わしくなるので、要注意です。

（場合Ｂの優れた別解）
　そのため、以下の樹形図を書いて枝の数を数えて確率を計算する方が、計算を楽にします。（○は偶数、×は奇数です）

（場合Ｂの別解２）
　先に作った樹形図では、最細枝の太さが揃っていないので、計算が若干面倒です。そのため、以下の樹形図のように、通算４回の偶数が出た後で空試行をすることにして試行回数を６回にそろえる。
すなわち、通算４回の偶数が出た事象：
(0,0,0,0)
を、試行回数が６回の以下の事象の連鎖４つに分ける。
(0,0,0,0,0,0)
(0,0,0,0,0,1)
(0,0,0,0,1,0)
(0,0,0,0,1,1)
そうすると、事象の連鎖の糸（枝）の太さがどの場合でも同じになり、計算が楽になります。

この樹形図を使って場合Ｂの幹の確率は以下の式で計算できます。

（場合Ｂの解答おわり）

（空試行の意味）
　以上の解き方において、空試行を行なうやり方の空試行の意味を以下で説明する。

　試行が終了した後でも、試行が終了しない場合の数と比較できるようにするために、
試行が終了した場合も、試行が終了しない場合と同じ回数の空の試行を続けるものとする。
　それにより、６回までのあらゆる組み合わせで細分化した最細枝の数は２の６乗＝６４本になる。

　６回以下で終了条件（偶数通算４回）を満たす場合を数える部分樹形図を書く。条件を満たした後でも空試行を続ける。
　空試行も含めた６回の試行で、偶数が通算４回以上（奇数は通算２回以下）になるのが場合Ｂである。
　場合Ｂを６回の試行での奇数の通算数で場合分けして場合の数（最細枝の本数）を数える。
　偶数（奇数）の通算数毎の、最細枝を成す６回の試行の事象の連鎖を以下に示す。

（１で奇数の事象を表し、０で偶数の事象を表す）
(0,0,0,0,0,0)　　奇数が０個の事象の連鎖は１本。
(0,1,0,0,0,0)　　奇数が１個の事象の連鎖は６本。
(0,1,0,0,1,0)　　奇数が２個の事象の連鎖は、

。
６回の試行の事象の連鎖の総数は、

本ある。

場合Ｂの部分樹形図を以下の図で書く。

この樹形図の場合の数（最細枝の数）に確率分の項を掛け算して場合Ｂの幹の確率を計算する。

（場合Ａの計算）
　この場合Ａの確率は、以下の樹形図を書いて計算することができる。

（補足）
　この樹形図は、枝の分岐の割合が、太さが単純に２分の１になったので、各枝の太さが簡単に計算できました。しかし、枝の分岐の割合が複雑な場合は、この図で各枝の太さの計算を繰り返すのが煩わしくなるので、要注意です。

（場合Ａの優れた別解）
　そのため、以下の樹形図を書いて枝の数を数えることで、計算を楽にします。（○は偶数、×は奇数です）

偶数でも奇数でも良い場合をＴとします。その場合の確率は１です。
上図の４つの場合は：
Ｘ，Ｘ，Ｘ：　確率は（１／２）の３乗
○，Ｘ，Ｘ，Ｘ：　確率は（１／２）の４乗
Ｔ，○，Ｘ，Ｘ，Ｘ：　確率は（１／２）の４乗
Ｔ，Ｔ，○，Ｘ，Ｘ，Ｘ：　確率は（１／２）の４乗
上図の４つの場合をチェックして、
偶数（○）が通算４回に達する場合が無いことを確認した。

（場合Ａの別解２）
　別解２として、試行が終了した後でも、試行が終了しない場合と比較できるようにするために、試行が終了した場合も、試行が終了しない場合と同じ回数の空の試行を続ける場合の樹形図を考えてみる。
（場合Ａでは、残念ながらこの別解２は、かえって解き方を難しくする）
その場合Ａの部分樹形図を以下の図で書く。

（注意）１つのイベントの結果の事象が奇数であるか偶数であるかを定めない最細枝（糸）の本数は、そのイベントの事象のバラエティに従って、事象が不定なイベント毎に２倍になる。
　ここで、
(1)６回行なう全部の組み合わせの数は２の６乗あります。
(2)偶数でも奇数でも良い場合をＴとします。その場合の数は２です。
(3)上図の４つの場合は：
Ｘ，Ｘ，Ｘ，Ｔ，Ｔ，Ｔ：　組み合わせの数は２の３乗
○，Ｘ，Ｘ，Ｘ，Ｔ，Ｔ：　組み合わせの数は２の２乗
Ｔ，○，Ｘ，Ｘ，Ｘ，Ｔ：　組み合わせの数は２の２乗
Ｔ，Ｔ，○，Ｘ，Ｘ，Ｘ：　組み合わせの数は２の２乗

上図の４つの場合の確率は：
Ｘ，Ｘ，Ｘ，Ｔ，Ｔ，Ｔ：　確率は（１／２）の３乗
○，Ｘ，Ｘ，Ｘ，Ｔ，Ｔ：　確率は（１／２）の４乗
Ｔ，○，Ｘ，Ｘ，Ｘ，Ｔ：　確率は（１／２）の４乗
Ｔ，Ｔ，○，Ｘ，Ｘ，Ｘ：　確率は（１／２）の４乗

　この４つの幹が分離されていて、それぞれが同時に生じることが無い、独立した組み合わせである事を確認するため、この４つの幹の構成をあらわす樹形図全体を、３回目の事象の分離から始めた下図の樹形図であらわした。