これは、ここをクリックした先の問題の解答です。
【問1】
A、B二人がコインを3枚ずつ持ち、じゃんけんして勝ったら相手からコイン一枚もらえ、先にどちらかのコインが無くなったらゲーム終了。
(ただし、あいこは回数には含まない。)
このとき、ちょうど9回で勝負が決まる確率を求めよ。
【解答1】
先ず、下図のように左から右に樹形図を書いて問題を整理します。
この樹形図の各枝は、事象の確率の太さを持ちます。この樹形図は、枝を束ねた合流点の節を持ちます。合流点の節では、その合流点の事象に至る樹形図の枝の確率の和の太さになります。
上図の樹形図に、分岐した枝の太さ(確率)と合流点の節の太さ(確率)を地道に書き込みます。
ここで、合流点の節から分岐する2つの枝の事象の確率は、どこから合流点に至ったかにかかわらず、1/2ずつです。
こうして枝の確率を地道に書いていくと、
Aが9回目に勝つ確率は
27÷29
になります。
よって、AかBかが9回目に勝つ確率=27×2÷29
=27×2-8
です。
(解答おわり)
【解答2】
(問題を解く方針)
場合の数を数え上げてこの問題を解く場合も、この樹形図(の一部)を書いて問題を図形化した上で、場合分けして、条件を満足する場合を地道に数えて答えを求めます。
Aが9回目に勝つ場合は、上のグラフの道を通ります。Aが9回目に勝つ全ての場合の数は、上のグラフの道の通り方の数になります。
9回目にAが勝つ場合の数と9回目にBが勝つ場合の数は等しいです。
求める確率は、
このグラフの道の通り方×2÷あらゆる場合の数
です。
あらゆる場合の数=2の9乗
です。
以下で、このグラフの道の通り方を、場合分けして地道に数え上げます。
以上の場合の合計は:
4+4+3+2+4+3+2+3+2=27
よって求める確率=27×2÷29
=27×2-8
(解答おわり)
【解答3】
この問題は、以下の図形に図形化したことが、問題を解くために本質的に重要でした。
解答2の樹形図の一部のグラフの道の通り方の数え方を、以下の様に工夫して数えてみます。
(解答はじめ)
Aが9回目に勝つ場合は、上のグラフの道を通ります。Aが9回目に勝つ全ての場合の数は、上のグラフの道の通り方の数になります。
9回目にAが勝つ場合の数と9回目にBが勝つ場合の数は等しいです。
求める確率は、
このグラフの道の通り方×2÷あらゆる場合の数
です。
あらゆる場合の数=2の9乗
です。
このグラフの道の通り方には、以下の2種類の場合があります。
(1)
(2)

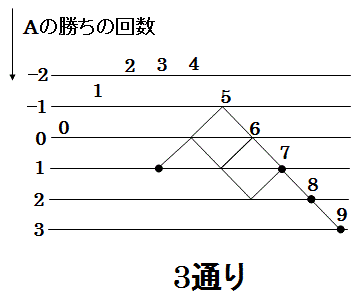
(2)の場合の図のy通りの通り方のyの値を、以下で場合分けして求めます。
(2-1)
(2-2)

よって、
y=3+2=5
です。
(3)
よってAが9回目に勝つ全ての場合の数は、
12+3y=12+15=27
です。
よって求める確率=27×2÷29
=27×2-8
(解答おわり)
リンク:
高校数学の目次
【問1】
A、B二人がコインを3枚ずつ持ち、じゃんけんして勝ったら相手からコイン一枚もらえ、先にどちらかのコインが無くなったらゲーム終了。
(ただし、あいこは回数には含まない。)
このとき、ちょうど9回で勝負が決まる確率を求めよ。
【解答1】
先ず、下図のように左から右に樹形図を書いて問題を整理します。
上図の樹形図に、分岐した枝の太さ(確率)と合流点の節の太さ(確率)を地道に書き込みます。
ここで、合流点の節から分岐する2つの枝の事象の確率は、どこから合流点に至ったかにかかわらず、1/2ずつです。
こうして枝の確率を地道に書いていくと、
Aが9回目に勝つ確率は
27÷29
になります。
よって、AかBかが9回目に勝つ確率=27×2÷29
=27×2-8
です。
(解答おわり)
【解答2】
(問題を解く方針)
場合の数を数え上げてこの問題を解く場合も、この樹形図(の一部)を書いて問題を図形化した上で、場合分けして、条件を満足する場合を地道に数えて答えを求めます。
Aが9回目に勝つ場合は、上のグラフの道を通ります。Aが9回目に勝つ全ての場合の数は、上のグラフの道の通り方の数になります。
9回目にAが勝つ場合の数と9回目にBが勝つ場合の数は等しいです。
求める確率は、
このグラフの道の通り方×2÷あらゆる場合の数
です。
あらゆる場合の数=2の9乗
です。
以下で、このグラフの道の通り方を、場合分けして地道に数え上げます。
以上の場合の合計は:
4+4+3+2+4+3+2+3+2=27
よって求める確率=27×2÷29
=27×2-8
(解答おわり)
【解答3】
この問題は、以下の図形に図形化したことが、問題を解くために本質的に重要でした。
解答2の樹形図の一部のグラフの道の通り方の数え方を、以下の様に工夫して数えてみます。
(解答はじめ)
Aが9回目に勝つ場合は、上のグラフの道を通ります。Aが9回目に勝つ全ての場合の数は、上のグラフの道の通り方の数になります。
9回目にAが勝つ場合の数と9回目にBが勝つ場合の数は等しいです。
求める確率は、
このグラフの道の通り方×2÷あらゆる場合の数
です。
あらゆる場合の数=2の9乗
です。
このグラフの道の通り方には、以下の2種類の場合があります。
(1)
(2)

(2)の場合の図のy通りの通り方のyの値を、以下で場合分けして求めます。
(2-1)
(2-2)

よって、
y=3+2=5
です。
(3)
よってAが9回目に勝つ全ての場合の数は、
12+3y=12+15=27
です。
よって求める確率=27×2÷29
=27×2-8
(解答おわり)
リンク:
高校数学の目次












分かりにく
返信削除