これは、ここをクリックした先のページの問題の解答です。
【問1】
上の三角形において、上の式が成り立つことを証明せよ。
【解答1】
先ず、式の右辺のhを三角関数であらわした上で正弦定理を使って変形します。
(証明おわり)
【解答2】ベクトルの内積を使った証明
(証明おわり)
この証明は、ベクトルCZを直線BOと円との交点Dを経由した2つのベクトルに分解して、ベクトルZとベクトルCZの内積の式を上の式の様に分解する。
そして、円周角の定理から、ベクトルwがベクトルzに垂直であって、ベクトルwとベクトルzの内積が0になる事を利用した。
この式は、複素数平面を使って証明する事もできます。
【解答3】複素数平面を使った証明
ベクトルの内積を複素数平面を利用して表現して以下の様に証明できます。
この式(1)の右辺は、ベクトルzとベクトルβの内積の2倍をあらわしている。それは、ベクトルzの虚軸に射影した長さ=三角形の高さにベクトルβの長さを掛け算した値になる。
(証明おわり)
リンク:
高校数学の目次
【問1】
【解答1】
先ず、式の右辺のhを三角関数であらわした上で正弦定理を使って変形します。
【解答2】ベクトルの内積を使った証明
この証明は、ベクトルCZを直線BOと円との交点Dを経由した2つのベクトルに分解して、ベクトルZとベクトルCZの内積の式を上の式の様に分解する。
そして、円周角の定理から、ベクトルwがベクトルzに垂直であって、ベクトルwとベクトルzの内積が0になる事を利用した。
この式は、複素数平面を使って証明する事もできます。
【解答3】複素数平面を使った証明
ベクトルの内積を複素数平面を利用して表現して以下の様に証明できます。
この式(1)の右辺は、ベクトルzとベクトルβの内積の2倍をあらわしている。それは、ベクトルzの虚軸に射影した長さ=三角形の高さにベクトルβの長さを掛け算した値になる。
(証明おわり)
リンク:
高校数学の目次

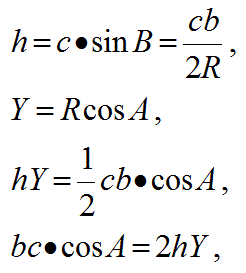
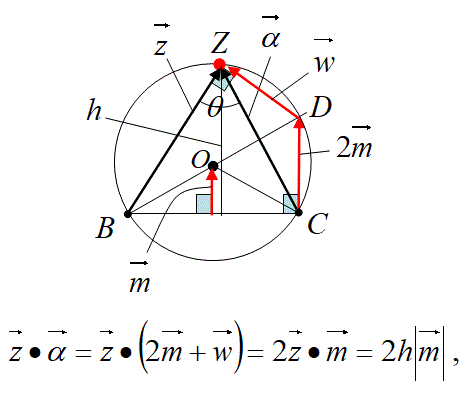

0 件のコメント:
コメントを投稿