これは、ここをクリックした先のページの問題の解答です。
【問1】
上の三角形ABCの外接円の中心O(外心)を原点にした座標系において、垂心Hの座標が、以下の式であらわされることを証明せよ。
【解答】

上図において、Hxについては、下の式が成り立っている。
そのため、残りのHyについて、問題の式が成り立つことを証明する。
以下の様に、図に書き込みを加えていく。
上図において、
△AHDと△BHEは、
∠AHD=∠BHE、
∠HDA=∠HEB
で二角が等しいので、
△AHD∽△BHE
である。
∴ ∠DAH=∠EBH ≡β
上図の
△BHEと△BFEは合同である。
(一辺BEを共有して等しく、その辺を挟む2角が等しいため)
合同な△BHEと△BFEの対応する辺EFとEHが等しく、
また、上図の点Fの座標が(Ax,-Ay)であり、
点Eの座標が (Cx,Cy)であることから、
EF=Cy+Ay
である。
よって、以下の式が成り立つ。
また、以下の式もなりたつ。
(証明おわり)
(補足)
なお、原点Oを中心として三角形ABCを所定角度で回転させると、その垂心も原点Oの回りに同じ角度で回転する。
そして、回転した座標に対して上のHx,Hyの式で計算した座標も同じ角度で回転するので、回転した垂心の座標に等しくなる。
よって、任意の向きのどの三角形ABCにおいても、上の式が外心Oを原点にした垂心の座標をあらわす。
(補足2)
また、外心Oを原点にした重心の座標はこの垂心の座標の3分の1になる式であらわせる。
また、重心の座標の計算式は、座標系の原点をどこに変えても変わらないが、 垂心の座標の計算式は、座標系の原点を外心O以外にした場合は、上の式と異なる式に変わります。
リンク:
高校数学の目次
【問1】
【解答】

上図において、Hxについては、下の式が成り立っている。
そのため、残りのHyについて、問題の式が成り立つことを証明する。
以下の様に、図に書き込みを加えていく。
上図において、
△AHDと△BHEは、
∠AHD=∠BHE、
∠HDA=∠HEB
で二角が等しいので、
△AHD∽△BHE
である。
∴ ∠DAH=∠EBH ≡β
上図の
△BHEと△BFEは合同である。
(一辺BEを共有して等しく、その辺を挟む2角が等しいため)
また、上図の点Fの座標が(Ax,-Ay)であり、
点Eの座標が (Cx,Cy)であることから、
EF=Cy+Ay
である。
よって、以下の式が成り立つ。
また、以下の式もなりたつ。
(補足)
なお、原点Oを中心として三角形ABCを所定角度で回転させると、その垂心も原点Oの回りに同じ角度で回転する。
そして、回転した座標に対して上のHx,Hyの式で計算した座標も同じ角度で回転するので、回転した垂心の座標に等しくなる。
よって、任意の向きのどの三角形ABCにおいても、上の式が外心Oを原点にした垂心の座標をあらわす。
(補足2)
また、外心Oを原点にした重心の座標はこの垂心の座標の3分の1になる式であらわせる。
また、重心の座標の計算式は、座標系の原点をどこに変えても変わらないが、 垂心の座標の計算式は、座標系の原点を外心O以外にした場合は、上の式と異なる式に変わります。
リンク:
高校数学の目次
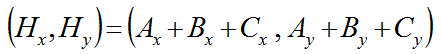





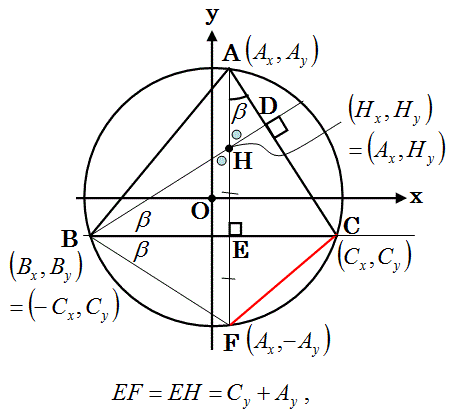
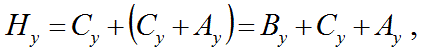

0 件のコメント:
コメントを投稿